{results_count} Math videos for {phrase}
Displaying {results_count} results of {results_count_total}
Solving Simple Quadratic Equations
🎬 Video Tutorial
(0:01) Solving Simple Quadratic Equations: For $x^2 = k$, there are two solutions: $x = \pm \sqrt{k}$. Note that $k$ must be non-negative, as $x^2$ cannot be negative.(1:26) No Real Solutions for Negative Numbers: If $k$ is negative, such as in $x^2 = -25$, there are no real solutions.(1:55) Solving $x^2 – d x = 0$ by Factorisation: Factor out $x$ to get $x(x – d) = 0$, giving solutions $x = 0$ and $x = d$.(2:45) A Common Pitfall: Avoid dividing both sides by $x$, as it can lead to missing solutions, especially $x = 0$.
📂 Revision Cards



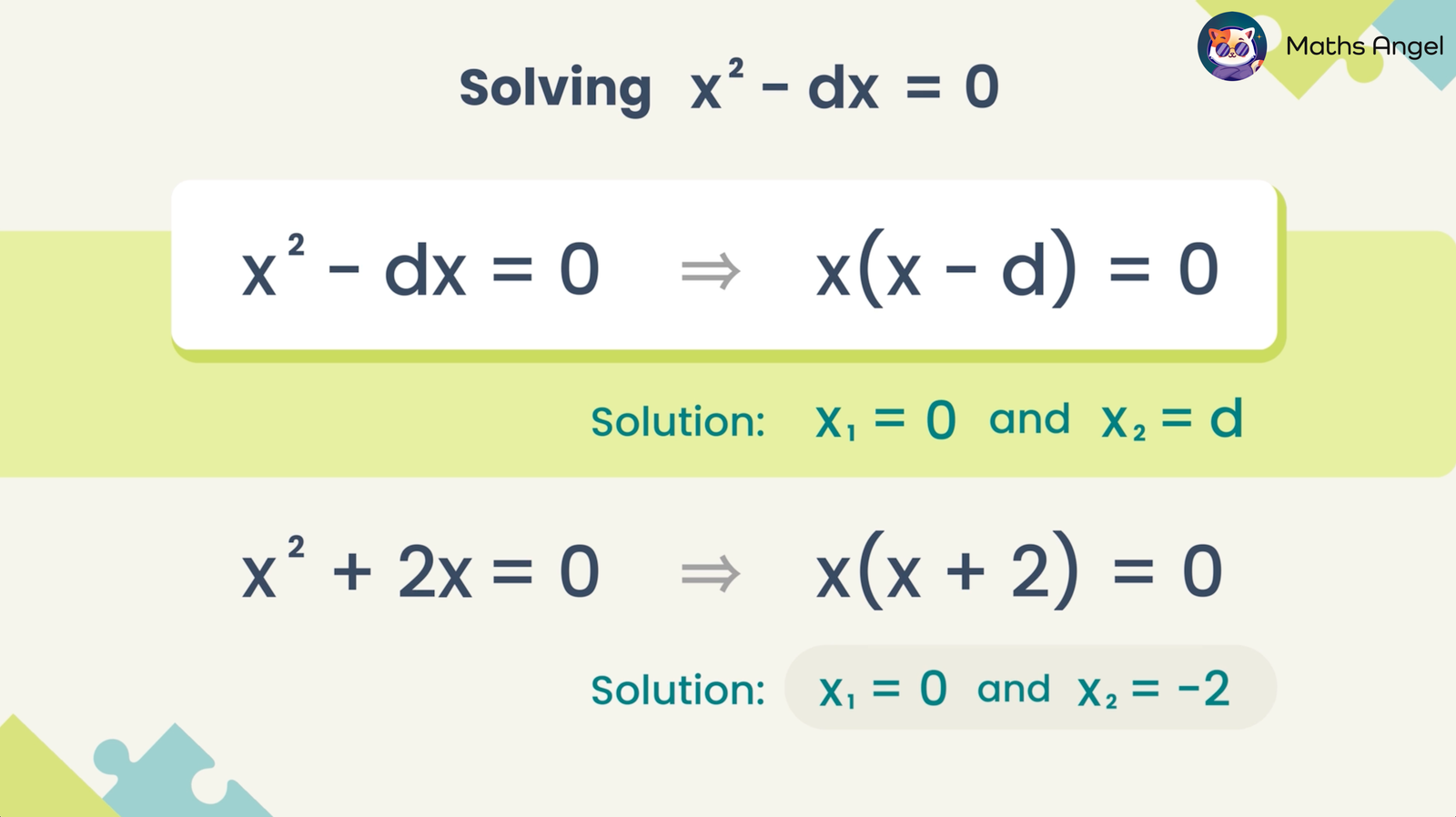


🍪 Quiz Time - Practice Now!
0%
🎩 AI Math Solver (ChatCat)
Need math help? Chat with our AI Math Solver at the bottom right!
0
0
votes
Article Rating
0 Comments
Newest
Oldest
Most Voted
Inline Feedbacks
View all comments

