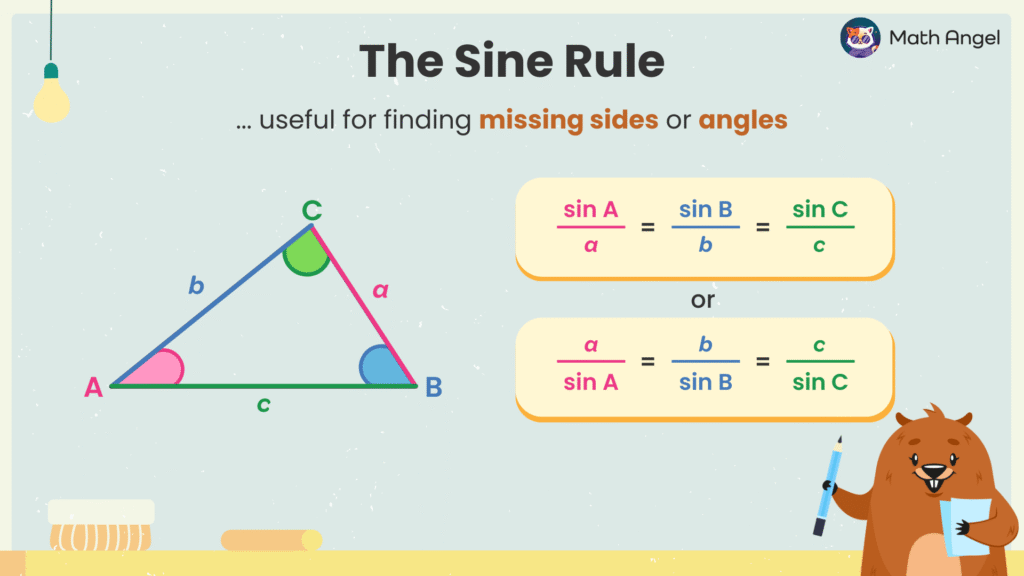
The Sine Rule helps find missing sides or angles in non-right-angled triangles.
🛎️ The Sine Rule Formula:
For any triangle with angles A, B, C and opposite sides a, b, c:
$$ \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} $$
or rearranged as:
$$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$
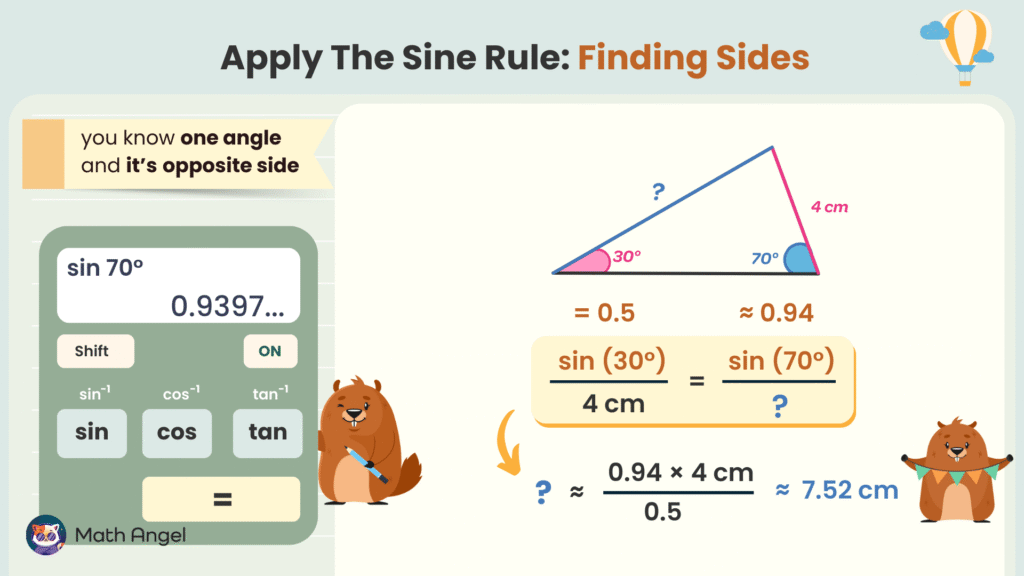
🛎️ When to Use the Sine Rule?
- To find a missing side when you know one side and two angles.
- To find a missing angle when you know two sides and one angle.