Geometry and Measures

Circumference and Area of a Circle and a Sector

Transformation and Symmetry

Line of Symmetry and Reflection Symmetry

Rotational Symmetry

Translating Shapes

Rotating Shapes

Trigonometry

Pythagoras Theorem

Trigonometry: Sine, Cosine, Tangent

2 of 2

Previous Lesson

{results_count} Math videos for {phrase}

Displaying {results_count} results of {results_count_total}

Generic filters

Exact matches only

Search in title

Search in content

Search in excerpt

Filter by Lesson Categories

Trigonometry: Sine, Cosine, Tangent

Geometry and Measures Trigonometry: Sine, Cosine, Tangent

Courses Overview

🎬 Video Tutorial

What are Sin, Cos, and Tan? (0:01)

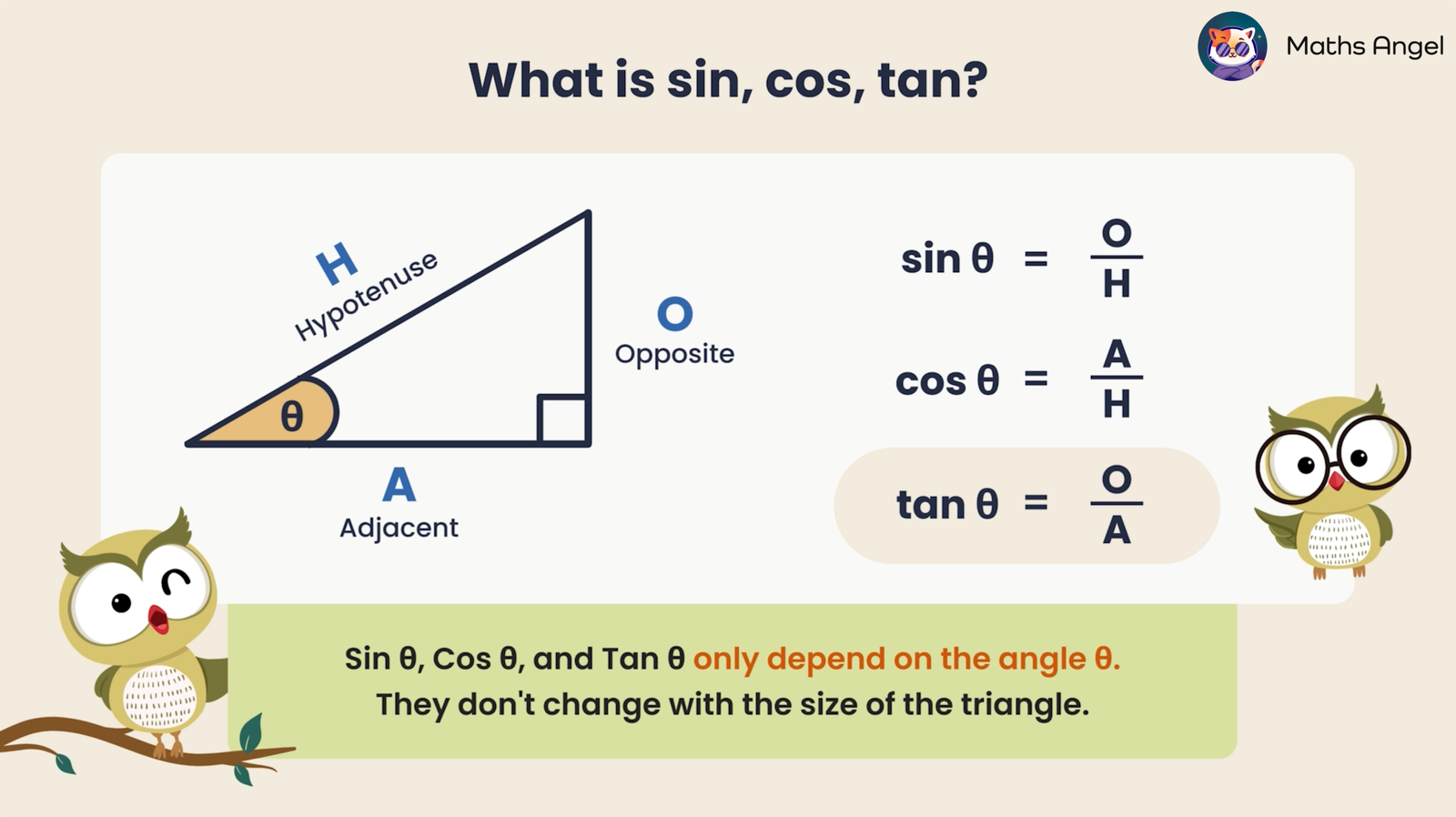
In a right-angled triangle, sine (sin), cosine (cos), and tangent (tan) are trigonometric ratios that compare two sides relative to a given angle θ:

Sine (sin θ) is the ratio of the opposite side of angle θ to the hypotenuse. $$\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}$$
Cosine (cos θ) is the ratio of the adjacent side of angle θ to the hypotenuse. $$\cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}}$$
Tangent (tan θ) is the ratio of the opposite side of angle θ to the adjacent side of angle θ. $$\tan \theta = \frac{\text{Opposite}}{\text{Adjacent}}$$

💡 SOH-CAH-TOA is an easy way to remember them!

🔑 Key Understanding: The values of sin θ, cos θ, and tan θ depend only on the angle θ, not the size of the triangle. Even if the triangle gets bigger or smaller, the ratios remain the same as long as the angle θ stays the same.

How to Use Sin to Find a Side? (0:56)

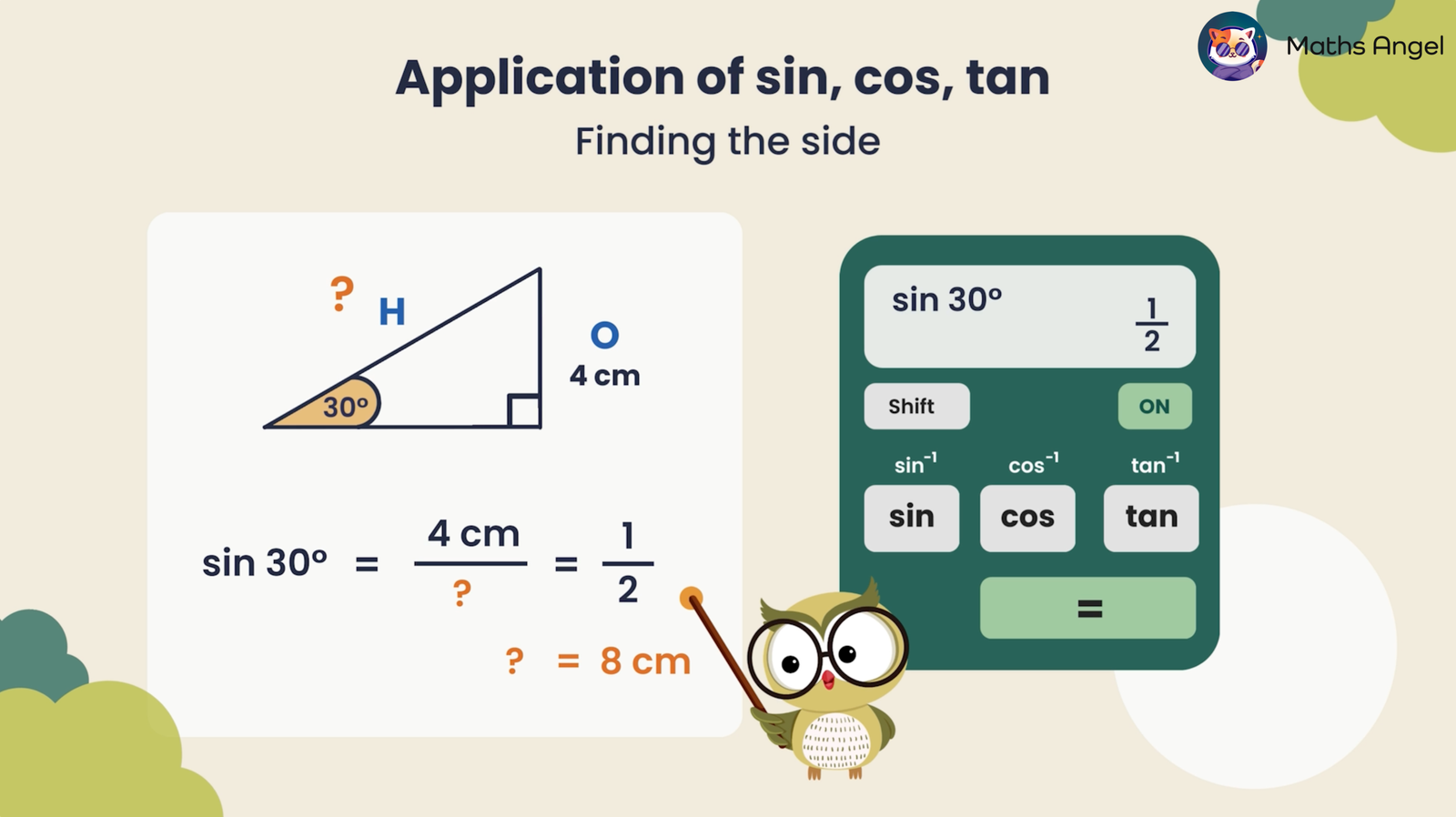
We can use sine to find a missing side in a right-angled triangle. If we are given:

Angle: $30^\circ$
Opposite side: $4 \text{ cm}$

To find the Hypotenuse, we use the sine formula: $\sin 30^\circ = \frac{4\text{ cm}}{\text{Hypotenuse}}$ Since $\sin 30^\circ = \large \frac{1}{2}$ $\text{Hypotenuse} = 4 \text{ cm} \times 2 = 8 \text{ cm}$

How to Use Tan to Find a Side? (1:40)

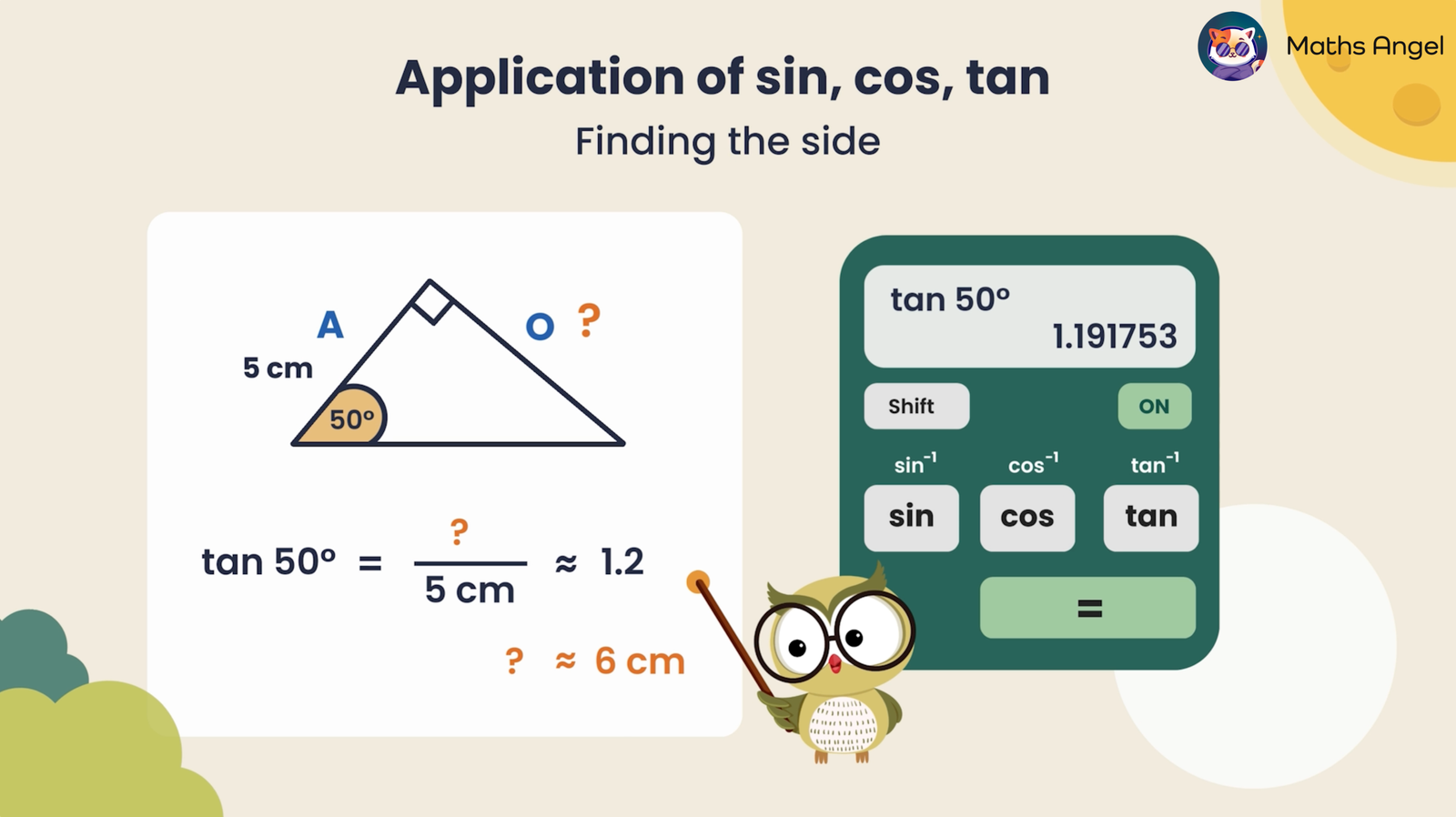
We can use tangent to find a missing side in a right-angled triangle. If we are given:

Angle: $50^\circ$
Adjacent side: $5 \text{ cm}$

To find the opposite side, we use the tangent formula: $$\tan 50^\circ = \frac{\text{Opposite}}{5 \text{ cm}}$$

Since $ \tan 50^\circ \approx 1.191753 $, we have:

$$\text{Opposite} \approx 5 \text{ cm} \times 1.191753 \approx 6 \text{ cm}$$

How to Use Cos to Find an Angle? (2:14)

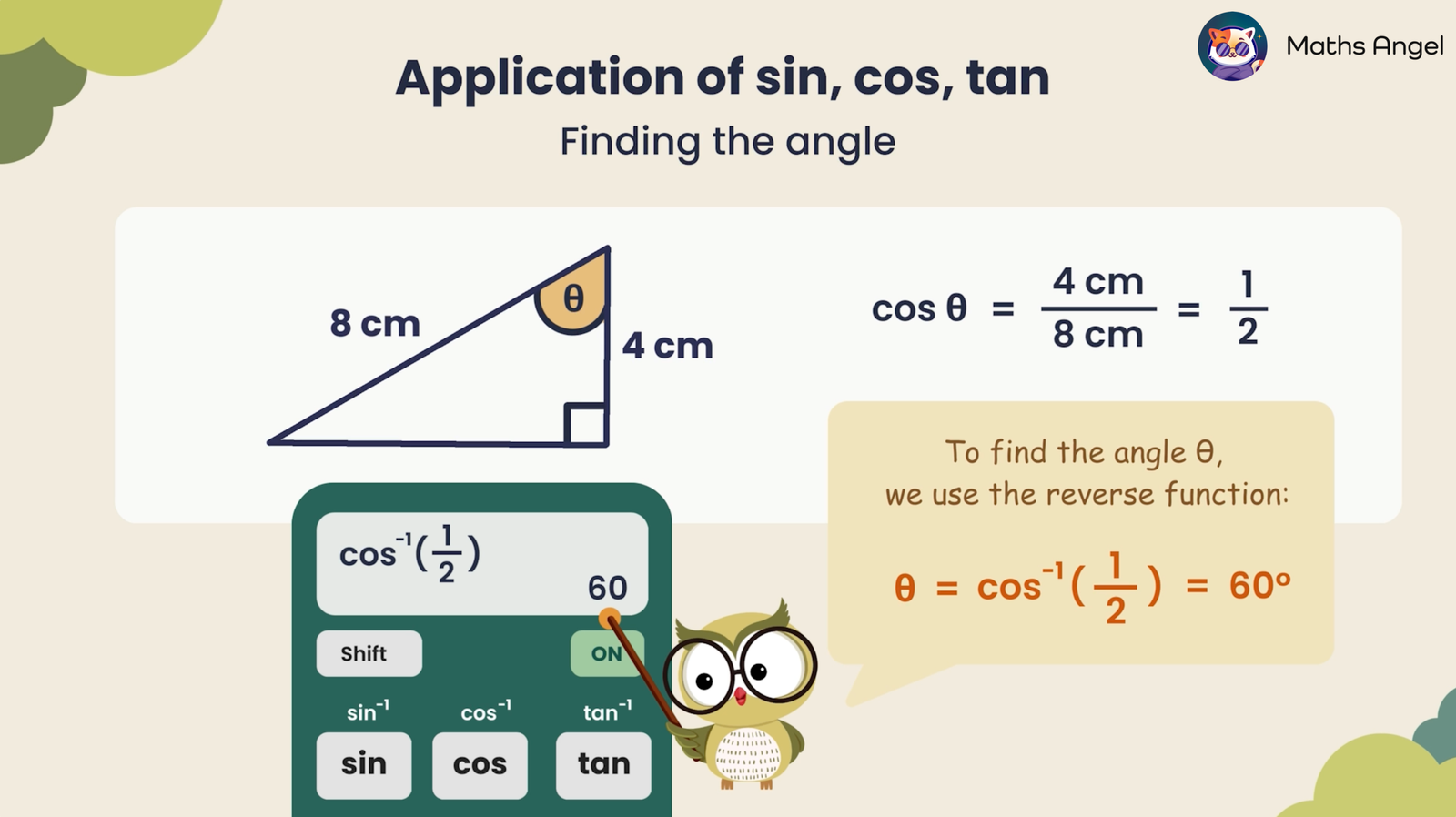
We can use cosine to find a missing angle in a right-angled triangle. If we are given:

Adjacent side: $4 \text{ cm}$
Hypotenuse: $8 \text{ cm}$

To find the angle $\theta$, we use the cosine formula: $$\cos \theta = \frac{4 \text{ cm}}{8 \text{ cm}} = \frac{1}{2}$$

Now, solve for $\theta$ by using the inverse cosine function:

$$\theta = \cos^{-1} \left(\frac{1}{2} \right)$$

Now, solve for $\theta$ by using the inverse cosine function on a calculator:

Press the cos⁻¹ button (If you can’t find it, press SHIFT, then COS)
Enter $\large \frac{1}{2}$ into the calculator.
Press =, and the calculator will display 60°

Thus, the missing angle is: $$\theta = 60^\circ$$

📂 Revision Cards

Definitions, ratios, and visuals of sine, cosine, and tangent shown in a right triangle. — 1) What is sin, cos, and tan?

A right triangle with 30° angle, opposite side 4 cm. Using the ratio of sin 30°, solve the hypotenuse, which is 8 cm. — 2) Trigonometry: Sine for Finding Side

The application of using tangent to find the missing side of a right triangle with a 50-degree angle and a known side of 5 cm. — 3) Trigonometry: Tangent for Finding Side

Finding the angle using cosine in a right triangle with sides 4 cm and 8 cm, showing the calculation cos ? = 1/2 and ? = cos?¹(1/2) = 60°. — 4) Trigonometry: Cosine for Finding Angle

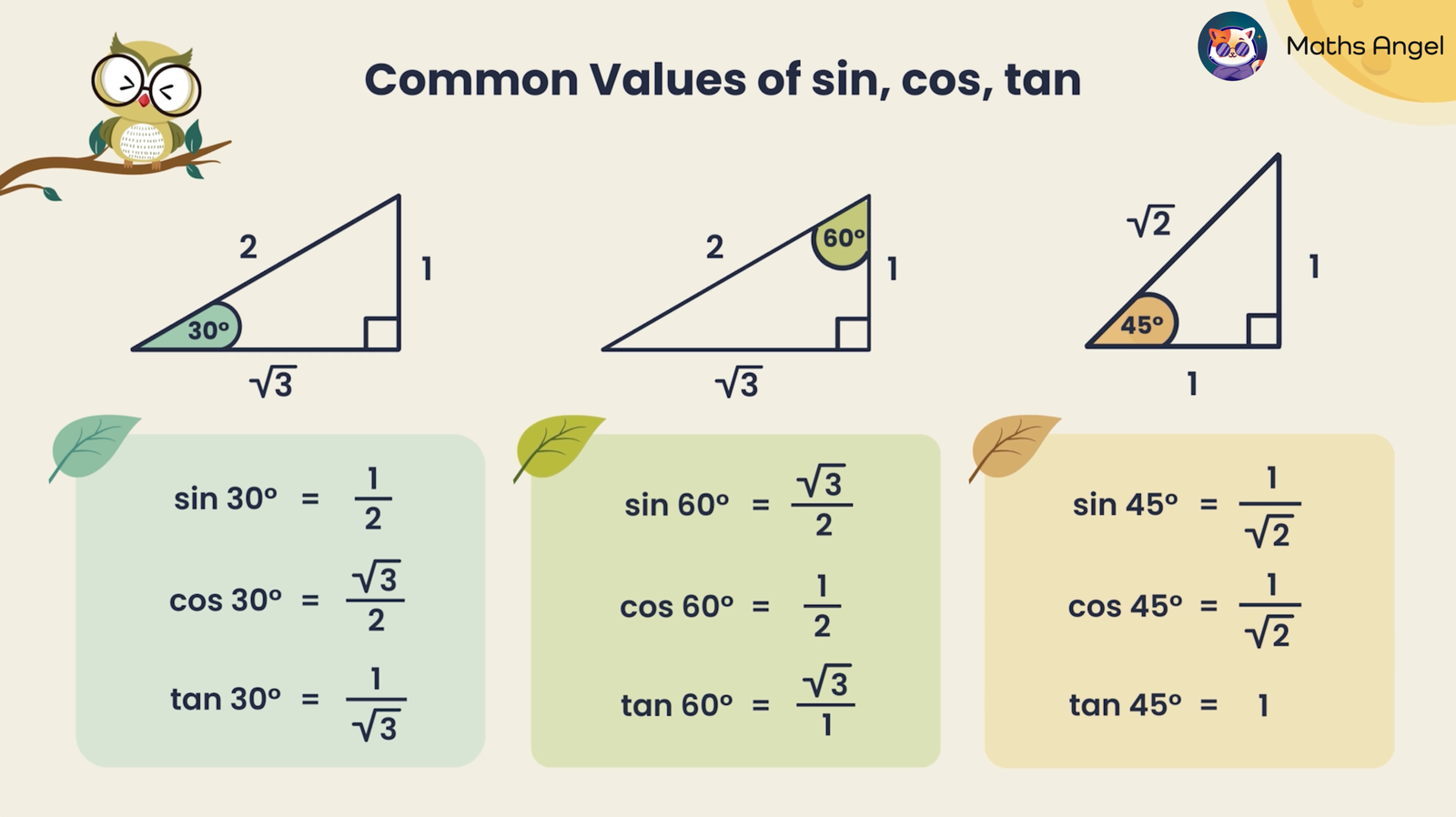
Common values of sine, cosine, and tangent for 30°, 60°, and 45° with right triangles and ratios. — 5) Trigonometry Table

🍪 Quiz Time - Practice Now!

0%

Trigonometry: Sine, Cosine, Tangent

1 / 6

Q: In a right-angled triangle, the opposite side is 3 cm, and the hypotenuse is 5 cm. What is the sine of the angle?

$\frac{4}{5}$

$\frac{5}{4}$

$\frac{3}{5}$

1

Feedback: Not quite! The sine formula is $sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$. Here, the opposite side is 3 cm and the hypotenuse is 5 cm. So, the sine of the angle is $ \frac{3}{5}$.

Feedback: Well done! The sine formula is $sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$. Here, the opposite side is 3 cm and the hypotenuse is 5 cm. So, the sine of the angle is $ \frac{3}{5}$.

2 / 6

Q: In a right-angled triangle, the adjacent side is 8 cm, and the hypotenuse is 10 cm. What is the cosine of the angle?

$\frac{4}{5}$

$\frac{5}{8}$

$\frac{7}{25}$

1

Feedback: Not quite! The cosine formula is $cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$. Here, the adjacent side is 8 cm and the hypotenuse is 10 cm. So, the cosine of the angle is $ \frac{8}{10} = \frac{4}{5}$.

Feedback: Well done! The cosine formula is $cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$. Here, the adjacent side is 8 cm and the hypotenuse is 10 cm. So, the cosine of the angle is $ \frac{8}{10} = \frac{4}{5}$.

3 / 6

Q: What is the sine of the angle?

$\frac{1}{2}$

1

$\frac{5}{8}$

$\frac{5}{16}$

Feedback: Not quite! The sine formula is $sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$. Here, the opposite side is 8 cm and the hypotenuse is 16 cm, so the sine of the angle is $ \frac{8}{16} = \frac{1}{2}$.

Feedback: Well done! The sine formula is $sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$. Here, the opposite side is 8 cm and the hypotenuse is 16 cm, so the sine of the angle is $ \frac{8}{16} = \frac{1}{2}$.

4 / 6

Q: What is the tangent of the angle?

$\frac{5}{13}$

$\frac{12}{13}$

$\frac{5}{12}$

$\frac{12}{5}$

Feedback: Not quite! Using the tangent formula $tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}$, here the opposite side is 5 cm and the adjacent side is 12 cm. So, the tangent of the angle is $ \frac{5}{12}$.

Feedback: Well done! Using the tangent formula $tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}$, here the opposite side is 5 cm and the adjacent side is 12 cm. So, the tangent of the angle is $ \frac{5}{12}$.

5 / 6

Q: What is the cosine of the angle?

$\frac{5}{12}$

$\frac{5}{13}$

$\frac{12}{5}$

$\frac{12}{13}$

Feedback: Not quite! Using the cosine formula $tan(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$, here the adjacent side is 12 cm and the hypotenuse side is 13 cm. So, the tangent of the angle is $ \frac{12}{13}$.

Feedback: Well done! Using the cosine formula $tan(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$, here the adjacent side is 12 cm and the hypotenuse side is 13 cm. So, the tangent of the angle is $ \frac{12}{13}$.

6 / 6

Q: Find the angle $\theta$ in the right-angled triangle.

$25^\circ$

$35^\circ$

$30^\circ$

$45^\circ$

Feedback: Not quite! The sine formula is $sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$. Here, the opposite side is 8 cm and the hypotenuse is 16 cm, so $sin(\theta) = \frac{8}{16} = \frac{1}{2}$. To find $\theta$, we use the inverse sine function. On a calculator, enter $sin^{-1}(\frac{1}{2})$, and it will give the result $\theta = 30^\circ$.

Feedback: Well done! The sine formula is $sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}$. Here, the opposite side is 8 cm and the hypotenuse is 16 cm, so $sin(\theta) = \frac{8}{16} = \frac{1}{2}$. To find $\theta$, we use the inverse sine function. On a calculator, enter $sin^{-1}(\frac{1}{2})$, and it will give the result $\theta = 30^\circ$.

Your score is

The average score is 39%

0%

🎩 AI Math Solver (ChatCat)

Need math help? Chat with our AI Math Solver at the bottom right!

Previous Lesson

3 Comments

Collapse Comments

5 2 votes

Article Rating

Label

Name*

Email

Label

Name*

Email

3 Comments

Newest

Oldest Most Voted

Inline Feedbacks

View all comments

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Comment *

Name

Email

Website

Save my name, email, and website in this browser for the next time I comment.

Log In

Username or Email Address

Password

Remember Me

Join Now | Lost Password?

Login

Accessing this course requires a login. Please enter your credentials below!

Username or Email Address

Password

Remember Me

Lost Your Password?

Register

Don't have an account? Register one!

Register an Account