Previous Lesson

Simple Quadratic Equations

Algebra and Graphs Simple Quadratic Equations

🎬 Video Tutorial

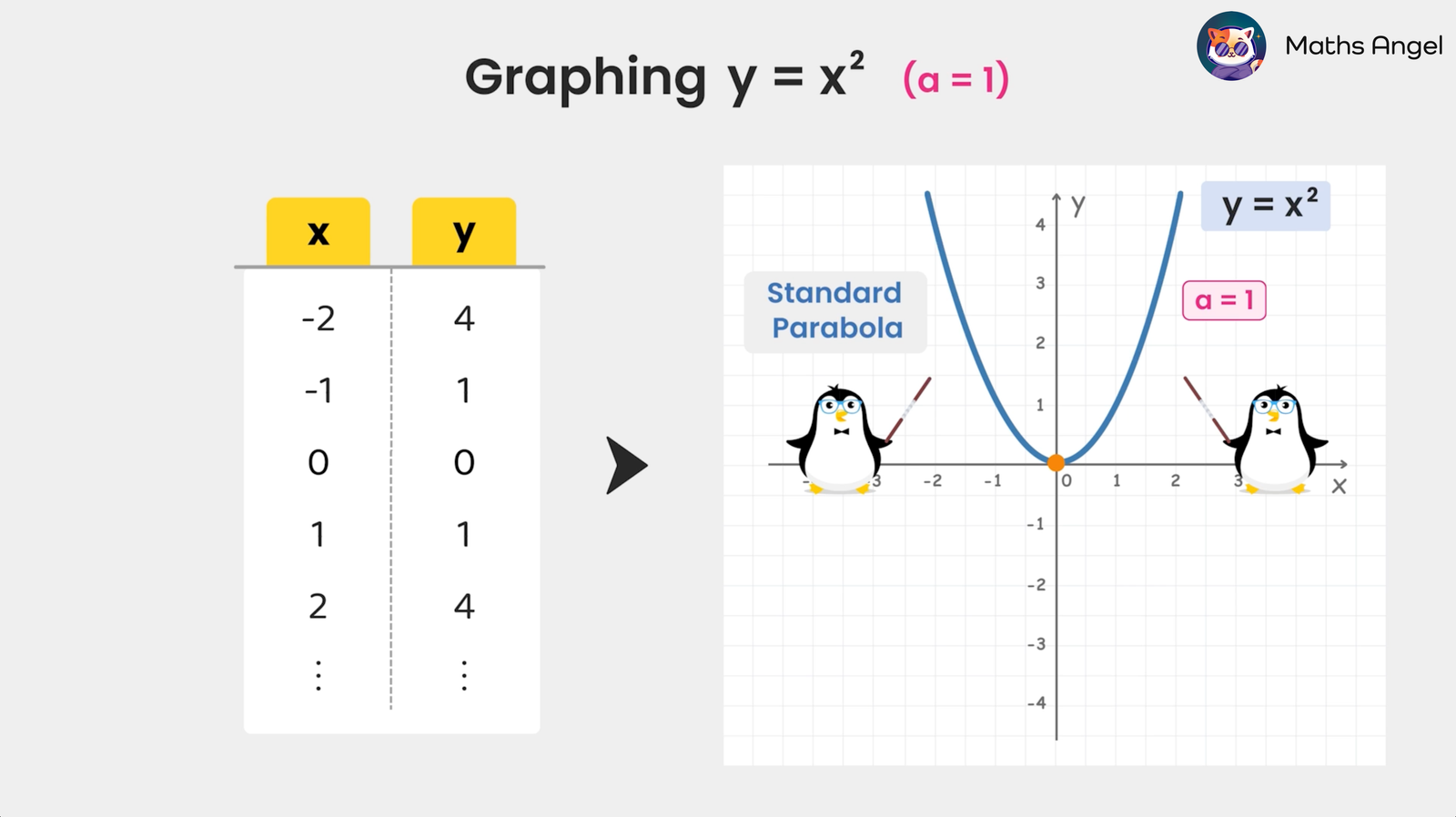
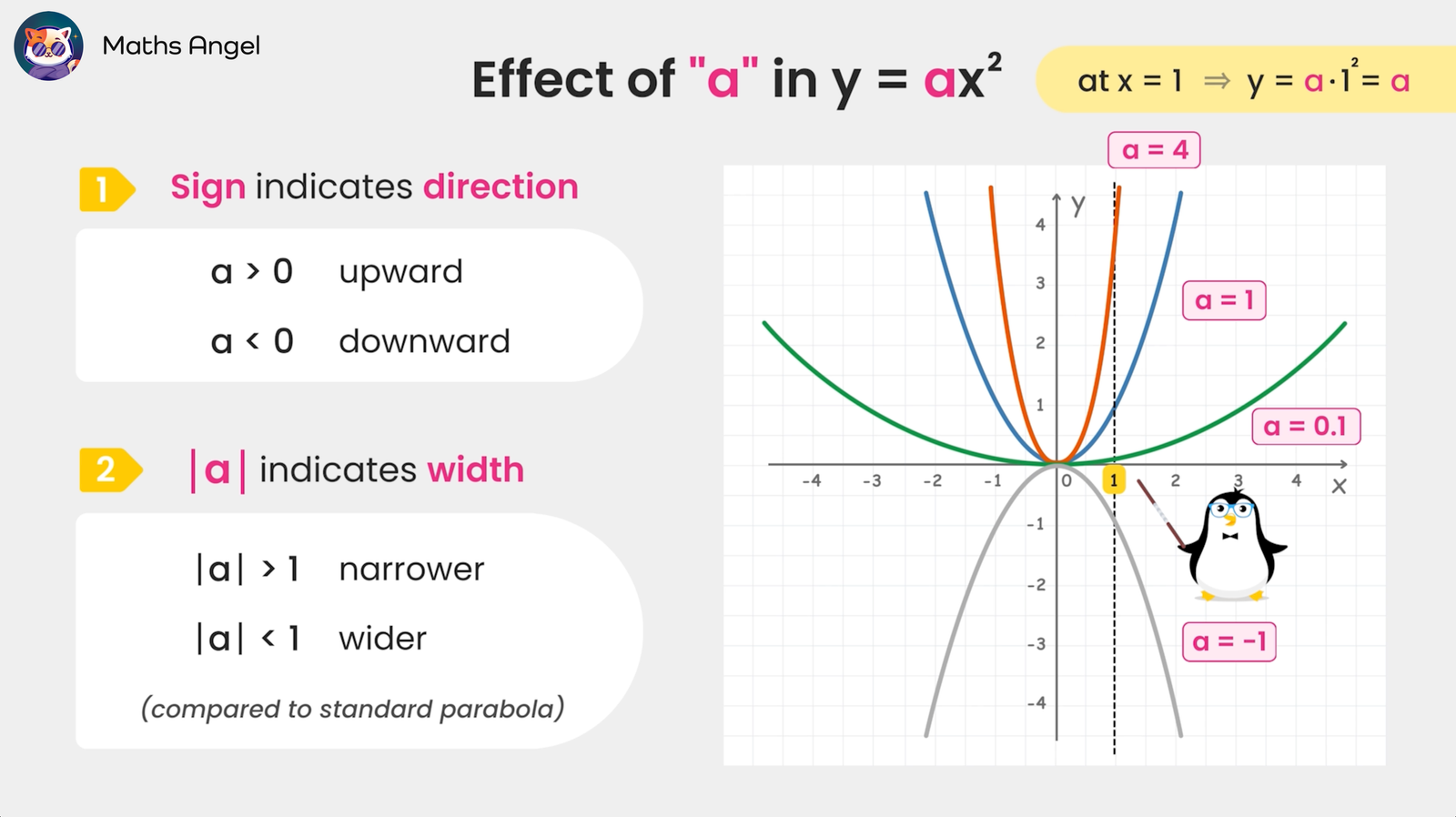
(0:01) Definition of Quadratic Equations: Quadratic equations contain an $x^2$ term; the standard form is $y = ax^2 + bx + c$ ($a \neq 0$).
(1:24) Role of Coefficient $a$: The sign of $a$ affects the parabola’s direction. If $a > 0$, the parabola opens upwards; if $a < 0$, it opens downwards.
(1:48) Effect of $|a|$ on Width: The larger the absolute value of $a$, the narrower the parabola. The smaller the absolute value of $a$, the wider the parabola.
(2:25) Vertex and Symmetry: For $y = ax^2$, the vertex is at $(0,0)$, and the parabola is symmetric about the $y$-axis because $x^2$ and $(-x)^2$ yield the same $y$-value.

Membership Required

You must be a member of Math Angel Plus or Math Angel Unlimited to view this content.

Already a member? Log in here

📂 Revision Cards

Quadratic equation formula y = ax² with a not equal to zero, highlighting coefficient 'a'.

Graph of the quadratic equation y = x² with a table of x and y values and a standard parabola on a coordinate plane where a = 1.

Graph illustrating how the sign of "a" affects direction and its absolute value affects the width of the parabola.

ChatCat (AI Math Tutor)

Previous Lesson

Related