Algebra and Graphs

Basic Expressions and Formulas

Introduction to Mapping

Introduction to Formulas

Deriving and Evaluating Expressions with One Variable

Equations and Simplifications

Simplifying Expressions

Solving Equations

Solving Rational Equations

Simplifying Expressions with Multiple Variables

Expanding and Binomials

Expanding Double Brackets

Square of a Binomial

Quadratic Equations

Simple Quadratic Equations

Vertex Form and Parabola Transformations

Converting Quadratics: Standard Form and Vertex Form

How to Write Quadratic Equations in Vertex Form and Standard Form

Solving Simple Quadratic Equations

Solving Quadratic Equations by Factorising

Solving Quadratic Equations: Quadratic Formula

Functions and Graphs

Plotting and Reflecting Points on the Coordinate Plane

Introduction to Functions and Graphs

Gradient and Y-Intercept in Linear Equations

Finding the Equation of a Straight Line

1 of 2

Previous Lesson

{results_count} Math videos for {phrase}

Displaying {results_count} results of {results_count_total}

Generic filters

Exact matches only

Search in title

Search in content

Search in excerpt

Filter by Lesson Categories

Vertex Form and Parabola Transformations

Algebra and Graphs Vertex Form and Parabola Transformations

Courses Overview

🎬 Video Tutorial

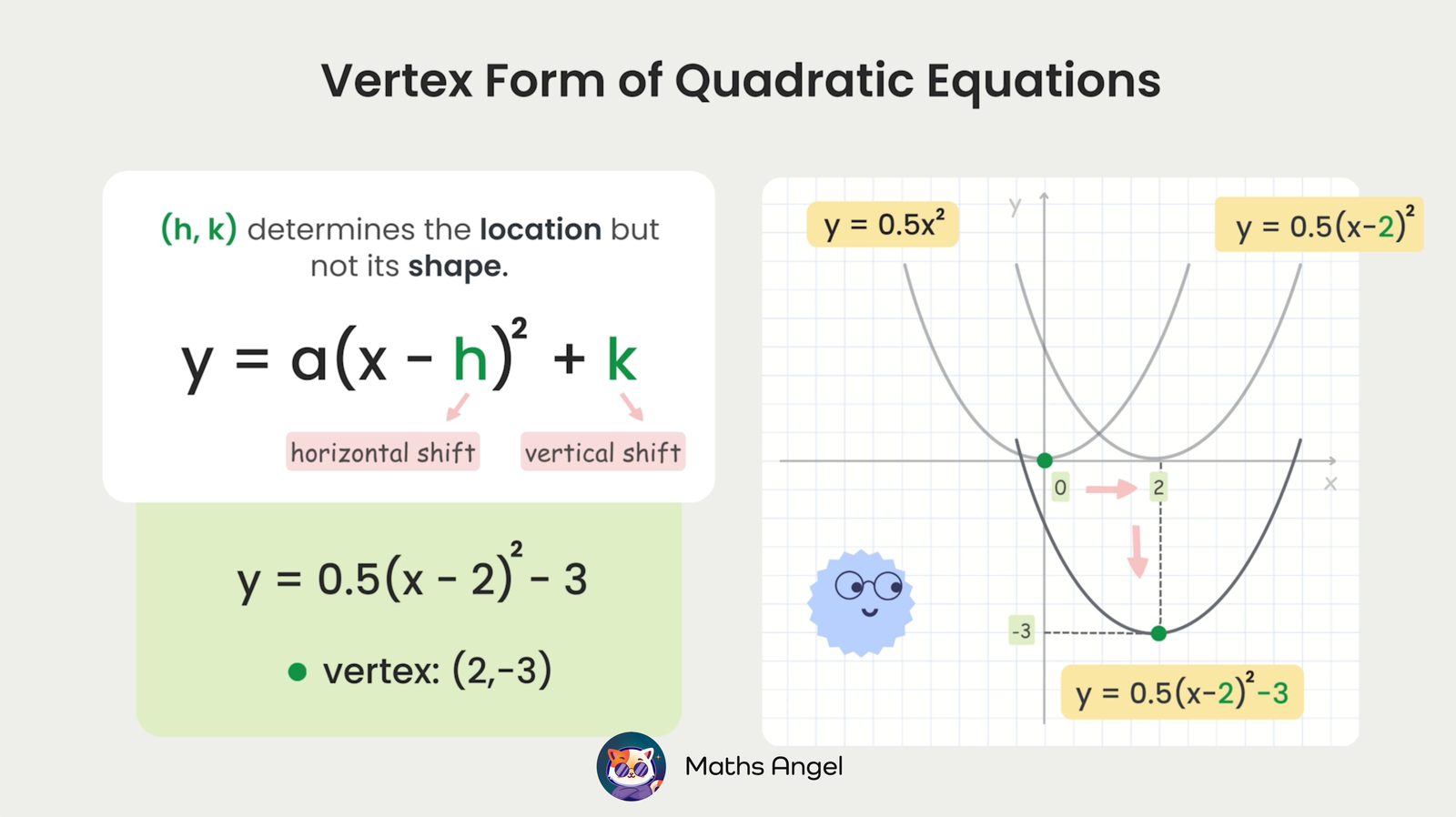
(0:01) Vertex Form of Quadratic Equations: The vertex form is $y = a(x – h)^2 + k$, where $(h, k)$ is the vertex of the parabola and $a \neq 0$. For example, in $y = 0.5 (x – 2)^2 – 3$, the vertex is $(2, -3)$.
(0:14) Vertex of a Parabola (The Turning Point): The vertex $(h, k)$ is the highest or lowest point. If $a > 0$, the parabola has a minimum at $x = h$ (opens upwards). If $a < 0$, it has a maximum at $x = h$ (opens downwards).
(1:28) Horizontal and Vertical Shift of the Parabola: Changing $h$ shifts the parabola horizontally (left or right), and changing $k$ shifts it vertically (up or down). As long as $a$ remains the same, the shape of the parabola remains consistent.

📂 Revision Cards

Vertex form of quadratic equation y = a(x - h)² + k, showing the vertex at point (h,k) on a graph of a parabola. — 1) Vertex Form of Quadratic Equations

Vertex form of quadratic equation y = a(x - h)² + k showing how horizontal (h) and vertical (k) shifts affect a parabola's position on a graph. — 2) Vertex Form Formula (h, k meaning)

Graph showing transformation of the quadratic equation from y = -2x² with vertex (0,0) to y = -2(x+2)² + 3 with vertex (-2,3), shifting the parabola. — 3) Shifting Parabola Using Vertex Form

🍪 Quiz Time - Practice Now!

0%

Vertex Form and Parabola Transformations

1 / 6

Q: In the vertex form of a quadratic equation, $y = a(x - h)^2 + k$, what does $h$ represent?

The vertical shift of the parabola

The shape of the parabola

The x-value that makes the expression 0

The y-value of the vertex

Feedback: Not quite! $h$ represents the x-value of the vertex, which makes the expression inside the brackets equal to zero. This value shifts the parabola horizontally along the x-axis.

Feedback: Well done! $h$ represents the x-value of the vertex, which makes the expression inside the brackets equal to zero. This value shifts the parabola horizontally along the x-axis.

2 / 6

Q: In the vertex form of a quadratic equation, $y = a(x - h)^2 + k$, what does $k$ represent?

The horizontal shift of the parabola

The x-value of the vertex

The shape of the parabola

The y-value of the vertex

Feedback: Not quite! $k$ represents the y-value of the vertex, which determines the vertical shift of the parabola.

Feedback: Well done! $k$ represents the y-value of the vertex, which determines the vertical shift of the parabola.

3 / 6

Q: In the quadratic equation $y = -3(x - 4)^2 + 7$, what is the vertex?

(4, 7)

(-4, -7)

(4, -7)

(-4, 7)

Feedback: Not quite! The vertex of the equation $y = -3(x - 4)^2 + 7$ is at (4, 7). To find this, look at the equation: the term $(x - 4)$ shows that $h = 4$. The number outside the brackets, 7, represents $k$. Therefore, the vertex is at (4, 7).

Feedback: Well done! The vertex of the equation $y = -3(x - 4)^2 + 7$ is at (4, 7). To find this, look at the equation: the term $(x - 4)$ shows that $h = 4$. The number outside the brackets, 7, represents $k$. Therefore, the vertex is at (4, 7).

4 / 6

Q: In the quadratic equation $y = 2(x + 3)^2 - 5$, what is the vertex?

(-3, 5)

(3, 5)

(3, -5)

(-3, -5)

Feedback: Not quite! The vertex of the equation $y = 2(x + 3)^2 - 5$ is at (-3, -5). To find this, look at the equation: the term $(x + 3)$ inside the brackets is equivalent to $(x - (-3))$, so $h = -3$. The number outside the brackets, -5, represents $k$. Therefore, the vertex is at (-3, -5).

Feedback: Well done! The vertex of the equation $y = 2(x + 3)^2 - 5$ is at (-3, -5). To find this, look at the equation: the term $(x + 3)$ inside the brackets is equivalent to $(x - (-3))$, so $h = -3$. The number outside the brackets, -5, represents $k$. Therefore, the vertex is at (-3, -5).

5 / 6

Q: In the quadratic equation $y = -4(x - 1)^2 + 6$, what is the vertex?

(1, -6)

(-1, -6)

(-1, 6)

(1, 6)

Feedback: Not quite! The vertex of the equation $y = -4(x - 1)^2 + 6$ is at (1, 6). To find this, observe that the term $(x - 1)$ shows that $h = 1$. The number outside the brackets, 6, represents $k$. Therefore, the vertex is at (1, 6).

Feedback: Well done! The vertex of the equation $y = -4(x - 1)^2 + 6$ is at (1, 6). To find this, observe that the term $(x - 1)$ shows that $h = 1$. The number outside the brackets, 6, represents $k$. Therefore, the vertex is at (1, 6).

6 / 6

Q: In the quadratic equation $y = -5(x + 5)^2 - 2$, find the highest point of the parabola?

(-5, -2)

(5, -2)

(5, 2)

(-5, 2)

Feedback: Not quite! Since the coefficient of $a$ is negative, the parabola opens downward, making the vertex the highest point. The term $(x + 5)$ indicates that $h = -5$, and the number outside the brackets, -2, represents $k$. Therefore, the highest point is at (-5, -2).

Feedback: Well done! Since the coefficient of $a$ is negative, the parabola opens downward, making the vertex the highest point. The term $(x + 5)$ indicates that $h = -5$, and the number outside the brackets, -2, represents $k$. Therefore, the highest point is at (-5, -2).

Your score is

The average score is 66%

0%

🎩 AI Math Solver (ChatCat)

Need math help? Chat with our AI Math Solver at the bottom right!

Previous Lesson

0 0 votes

Article Rating

Label

Name*

Email

Label

Name*

Email

0 Comments

Newest

Oldest Most Voted

Inline Feedbacks

View all comments

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Comment *

Name

Email

Website

Save my name, email, and website in this browser for the next time I comment.

Log In

Username or Email Address

Password

Remember Me

Join Now | Lost Password?

Login

Accessing this course requires a login. Please enter your credentials below!

Username or Email Address

Password

Remember Me

Lost Your Password?

Register

Don't have an account? Register one!

Register an Account