Translating Shapes

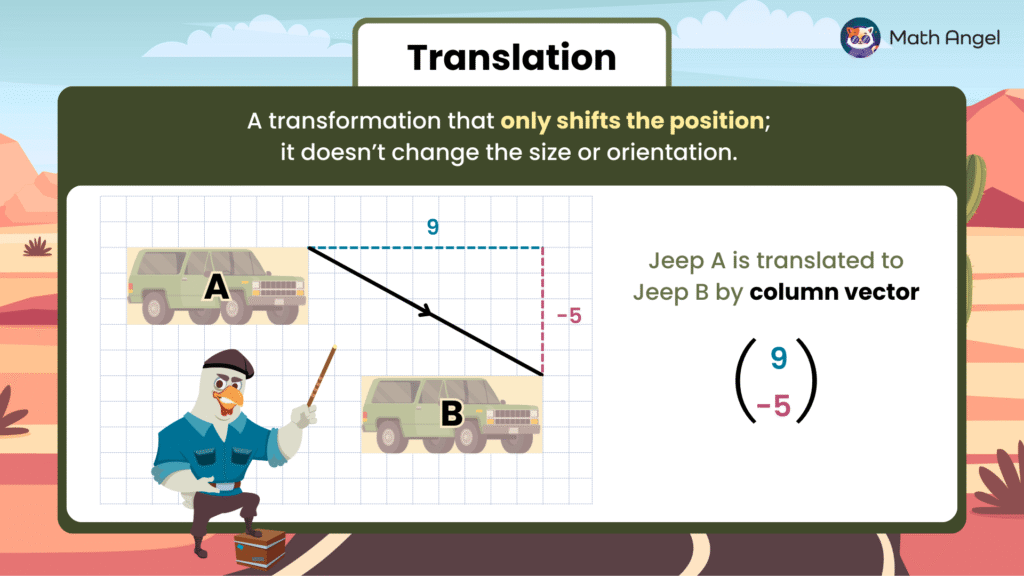
🌟 Translating Shapes in Math:

A translation is a type of transformation that moves (shifts) a shape to a new position.

Importantly, a translation only changes the shape’s location. A translation does NOT change the shape’s size, shape, or direction.

🌟 How to Describe a Translation:

For example, shape A is moved 9 units to the right and 5 units down to become Shape B. This movement is a translation.

We describe this translation using a column vector:

$$
\begin{pmatrix}
9 \\
-5
\end{pmatrix}
$$

• The top number (9) means move 9 units to the right.
• The bottom number (-5) means move 5 units down.

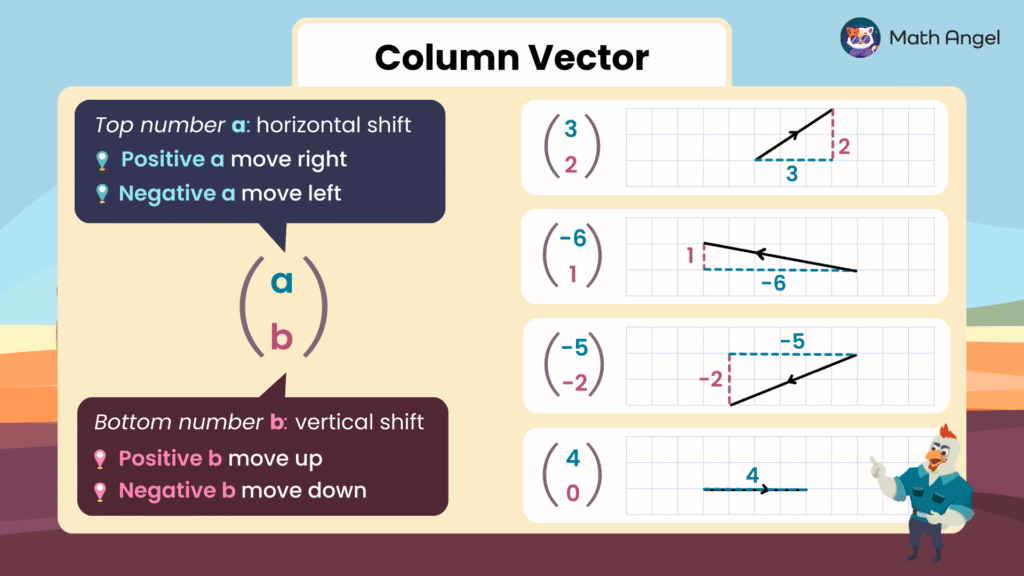
🌟 Definition of Column Vectors:

A column vector is a pair of numbers written vertically, like this:

$$
\begin{pmatrix}
a \\
b
\end{pmatrix}
$$

In math, we use column vectors to describe translations on a grid.

• Top number a: move horizontally
  • Positive $ a $: move right
  • Negative $ a $: move left
• Bottom number b: move vertically
  • Positive $ b $: move up
  • Negative $ b $: move down

🌟 Examples of Column Vectors:

• $\begin{pmatrix} 3 \\ 2 \end{pmatrix}$ means move 3 right and 2 up.

• $\begin{pmatrix} -6 \\ 1 \end{pmatrix}$ means move 6 left and 1 up.

• $\begin{pmatrix} -5 \\ -2 \end{pmatrix}$ means move 5 left and 2 down.

• $\begin{pmatrix} 4 \\ 0 \end{pmatrix}$ means move 4 right and do not move up or down.

🔮 How does a vector look on a grid?

A vector is shown as an arrow from the starting point to the ending point.

In math exams, if you see an arrow on the grid, you should be able to write its column vector by counting how many units it moves right or left, and up or down.

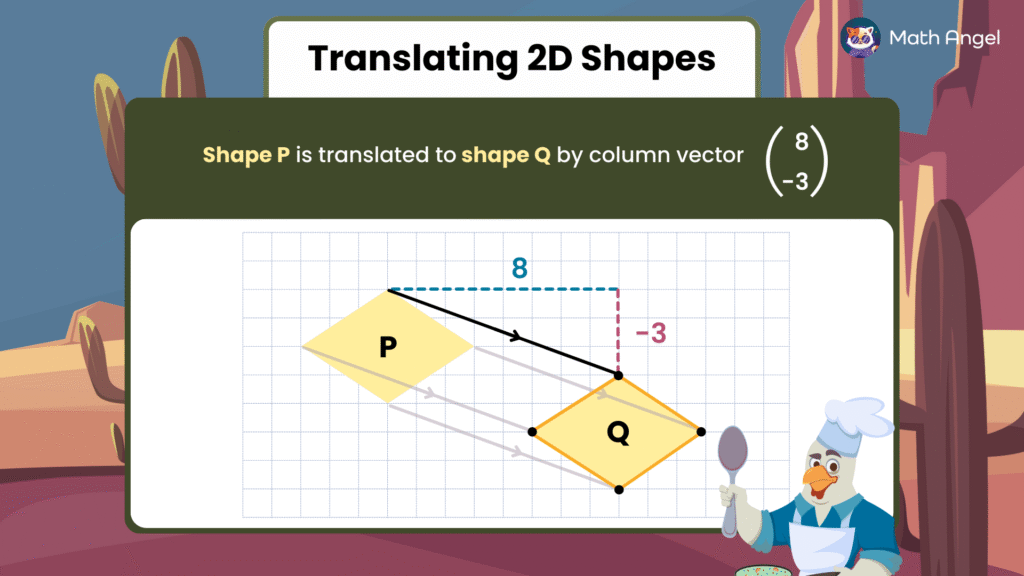
Task:
Translate Shape P to Shape Q by the column vector:

$$
\begin{pmatrix}
8 \\
-3
\end{pmatrix}
$$

This means:
Every point (corner) of Shape P moves 8 units to the right and 3 units down.

Steps to Translate:

1. Move each corner (vertex) of Shape P according to the column vector: 8 units right, 3 units down.

2. After moving all the corners, connect them in the same order to make the new shape (Shape Q).

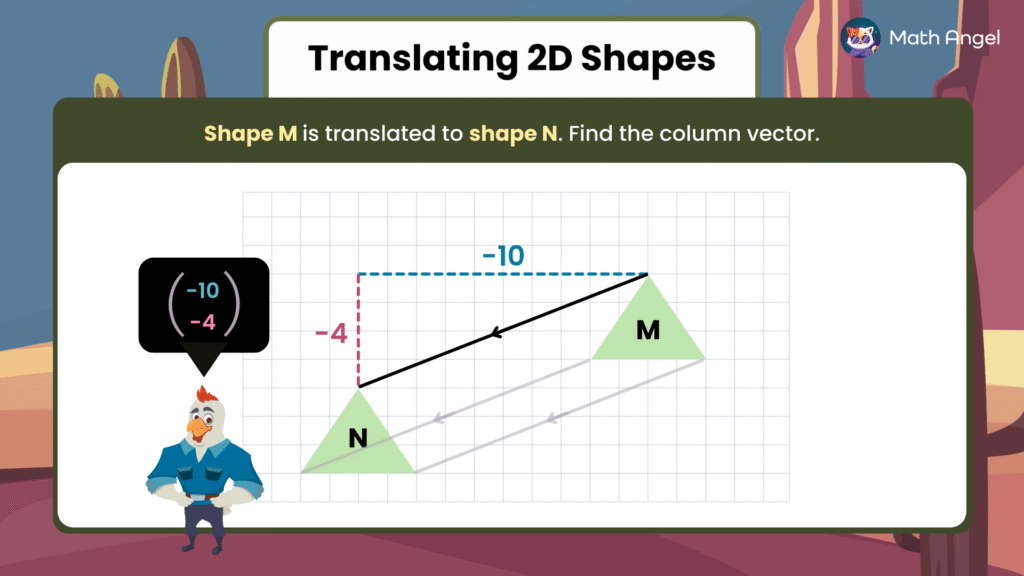
Task:
Shape M is translated to Shape N. What is the column vector?

Steps:

• Step 1: Pick any matching corner on both shapes (for example, the top point of M and N).
• Step 2: Count how many units right/left and up/down you need to move to go from M to N:
  • Move 10 units left: $-10$
  • Move 4 units down: $-4$

Final Answer:
The column vector is

$$
\begin{pmatrix}
-10 \\
-4
\end{pmatrix}
$$

This means every point on M moves 10 units left and 4 units down to become shape N.