Square of a Binomial
Table Of Contents
🎬 Math Angel Video: 3 Key Formulas for Product of Binomials
Formula for Squaring a Binomial
⏩️
🛎️ What is a Binomial?
A binomial is an algebraic expression with two terms, like $ (a + b) $.
🛎️ How Do You Square a Binomial?
- To square $ (a + b) $, multiply it by itself: $$ (a + b)^2 = (a + b)(a + b) $$
- Using distribution: $$ a \cdot a + a \cdot b + b \cdot a + b \cdot b $$
- Then, use exponents and combine like terms: $$ a^2 + 2ab + b^2 $$
- Thus, the formula for squaring a binomial is: $$ (a + b)^2 = a^2 + 2ab + b^2 $$
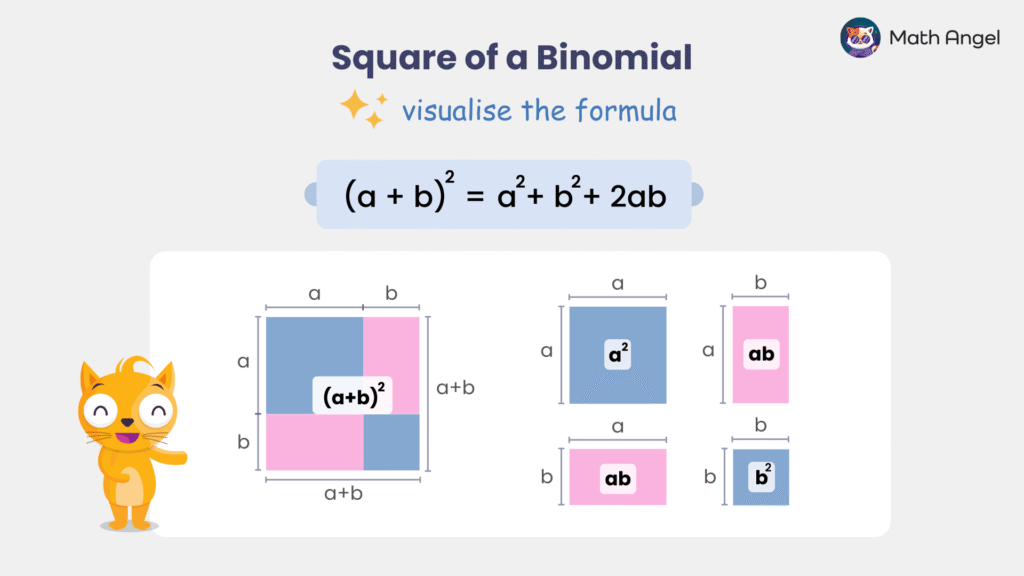
Visualizing the Perfect Square Formula
⏩️
Instead of expanding algebraically, let’s understand $ (a + b)^2 $ geometrically.
Step 1: Consider a square with side length $ (a + b) $. The total area is:
$$ (a + b) \times (a + b) $$
Step 2: Divide this large square into four smaller rectangles:
- A square of area $ a^2 $
- A square of area $ b^2 $
- Two identical rectangles, each with area $ ab $
Step 3: Adding all four regions together:
$$ a^2 + 2ab + b^2 $$
Since these four areas make up the entire large square, we conclude:
$$ (a + b)^2 = a^2 + 2ab + b^2 $$
3 Key Formulas for Squaring Binomials
⏩️
🛎️ Square of a Sum Formula:
$ (a + b)^2 = a^2 + b^2 + 2ab $
🛎️ Square of a Difference Formula:
$ (a\, -\, b)^2 = a^2 + b^2\, -\, 2ab $
🛎️ Difference of Squares Formula:
$ (a + b)(a\, -\, b) = a^2\, -\, b^2 $
These formulas help you expand, factor, and simplify expressions with ease!
How to Calculate the Square of a Sum (Example)
⏩️
Let’s apply the formula to expand $ (-2x + 3)^2 $.
- First, recall the formula:
$$ (a + b)^2 = a^2 + b^2 + 2ab $$ - Identify $ a $ and $ b $
$$ a = -2x $$ $$ b = 3 $$ - Substituting into the formula:
$$
\begin{aligned}
(-2x + 3)^2 &= (-2x)^2 + 3^2 + 2 \times (-2x) \times 3 \\[5pt]
&= 4x^2 + 9\, -\,12x
\end{aligned}
$$
❇️ Exam Tip: Watch out for negative signs when you substitute, especially when squaring or multiplying them.
How to Calculate the Square of a Difference (Example)
⏩️
Let’s apply the formula to expand $ (5x – 2y)^2 $.
- First, recall the formula:
$$ (a – b)^2 = a^2 + b^2 – 2ab $$ - Identify $ a $ and $ b $:
$$ a = 5x $$ $$ b = 2y $$ - Substituting into the formula:
$$
\begin{aligned}
(5x – 2y)^2 &= (5x)^2 + (2y)^2 – 2 \times (5x) \times (2y) \\[5pt]
&= 25x^2 + 4y^2 – 20xy
\end{aligned}
$$
❇️ Exam Tip: Include the correct signs and coefficients when identifying $ a $ and $ b $.
A missing negative or coefficient is one of the most common mistakes.
How to Apply Difference of Squares Formula (Example)
⏩️
Let’s apply the formula to expand $ (3x + 4)(3x – 4) $.
- First, recall the formula:
$$ (a + b)(a – b) = a^2 – b^2 $$ - Identify $ a $ and $ b $:
$$ a = 3x $$ $$ b = 4 $$ - Substituting into the formula:
$$
\begin{aligned}
(3x + 4)(3x – 4) &= (3x)^2 – 4^2 \\[5pt]
&= 9x^2 – 16
\end{aligned}
$$
❇️ Exam Tip: The middle terms cancel out in a difference of two squares. Check that your final answer only has two terms. If there’s an $xy$ or $x$ term left, you’ve made a mistake.
🍪 Quiz (6 Questions): Practice Square of a Binomial
🎩 Stuck on Expanding Binomials? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
