Gradient and Y-Intercept in Linear Equations

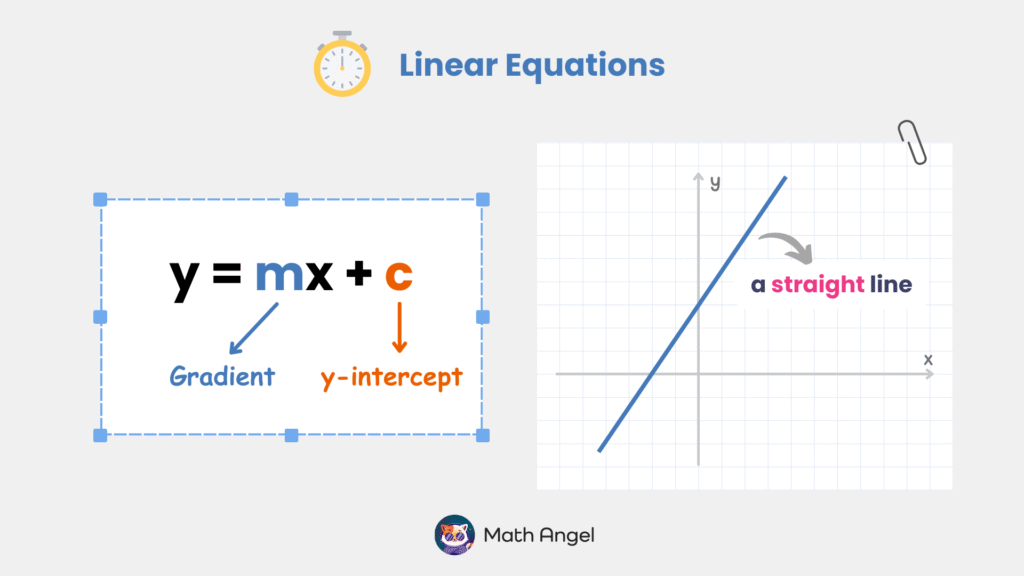
A linear equation is an equation that represents a straight-line relationship between variables. It follows the form:

$$ y = mx + c $$

where:

• $ m $ is the gradient (slope), which determines the steepness of the line.
• $ c $ is the y-intercept, where the line crosses the y-axis.

The graph of a linear equation always forms a straight line. Linear equations are fundamental in algebra and widely used in real-life applications.

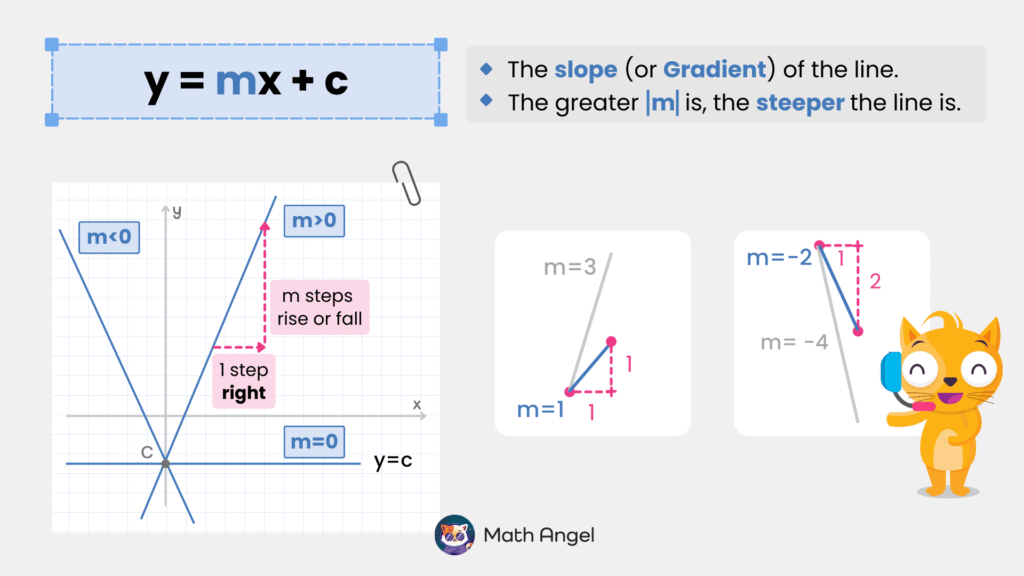
$ m $ is the the gradient (also called the slope) of a linear equation determines the steepness and direction of the line.

The gradient $ m $ tells us how much the value of $ y $ changes when $ x $ increases by 1.

• If $ m > 0 $, the line slopes upward (from left to right)
• If $ m < 0 $, the line slopes downward (from left to right)
• If $ m = 0 $, the line is horizontal
• The greater the absolute value of $ m $, the steeper the line.

Examples:

• When $ m = 1 $, the line rises 1 unit up for every 1 unit right.
• When $ m = 3 $, the line rises 3 units up for every 1 unit right.
• When $ m = -2 $, the line falls 2 units down for every 1 unit right.

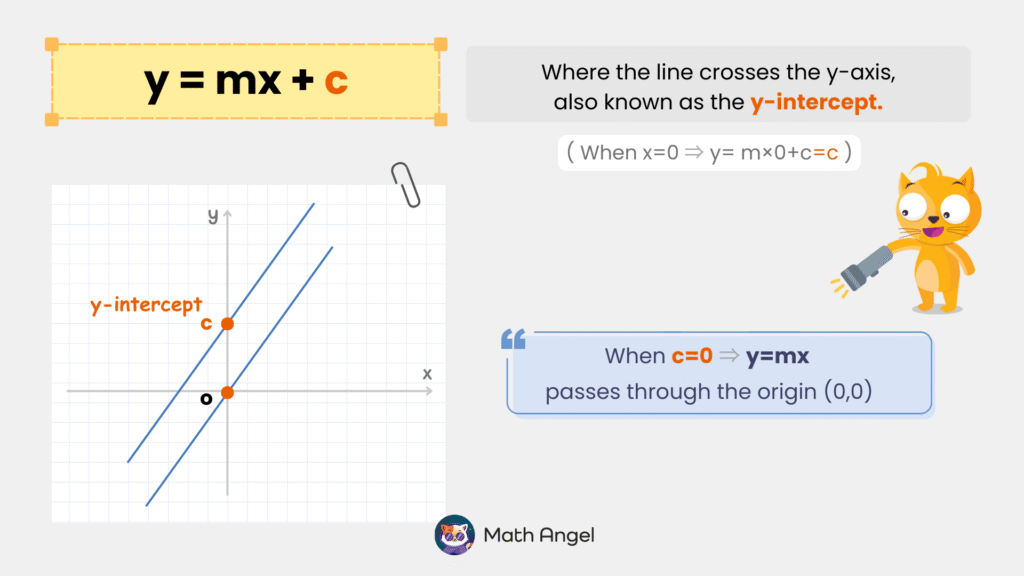
The y-intercept of a linear equation is the point where the line crosses the y-axis.

The y-intercept is found by setting $ x = 0 $ in the equation:

$$ y = m \cdot 0 + c = c $$

This means the y-intercept at the point $ (0, c) $. The y-intercept determines where the line starts on the y-axis, shifting the line up or down without changing its slope.