Area of a Trapezium
Table Of Contents
🎬 Math Angel Video: Finding the Area of a Trapezium
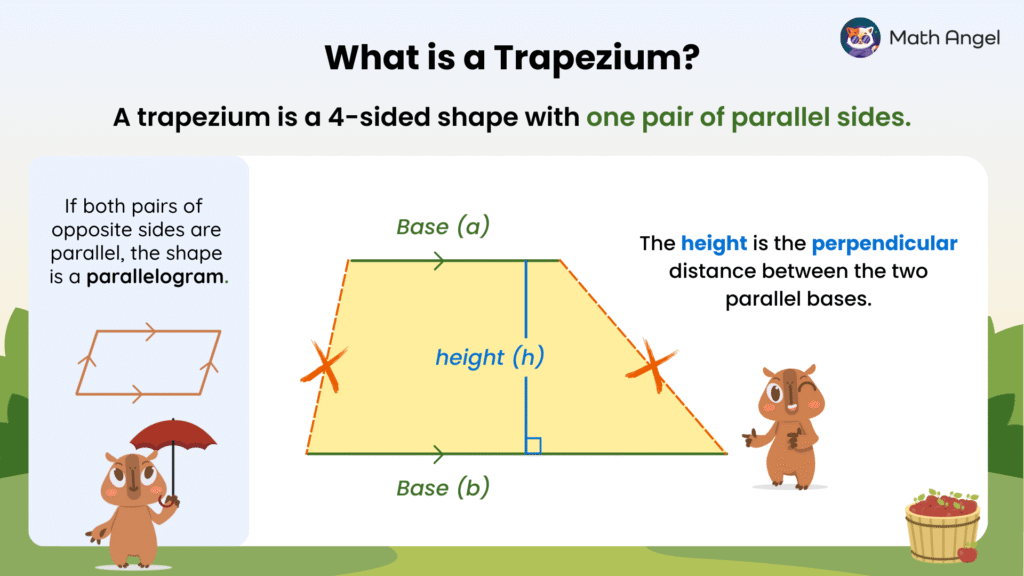
What Is a Trapezium?
⏩️
🛎️ Definition of A Trapezium:
A trapezium (also called a trapezoid) is a four-sided shape with only one pair of parallel sides.
- We call these parallel sides the bases.
- The other two sides are not parallel.
❇️ Note: If both pairs of opposite sides were parallel, the shape would be a parallelogram instead.
🛎️ Height of a Trapezium:
The height of a trapezium is the perpendicular distance between the two bases. The height must meet both bases at a right angle (90°).
🚨 Important: The height is not the length of the slanted sides. A common mistake is to use one of the non-parallel sides as the height. Don’t do this! 😵💫
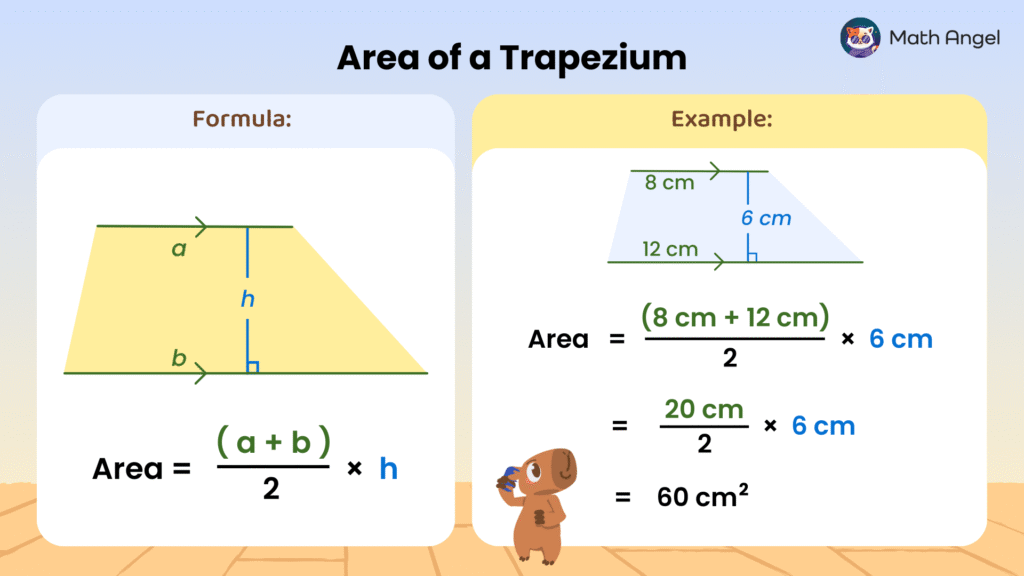
Formula for the Area of a Trapezium
⏩️
🛎️ Trapezoid Area Formula:
$$\text{Area} = \frac{\text{Base}_1 + \text{Base}_2}{2} \times \text{Height}$$
Follow these steps:
- Add the lengths of the two bases.
- Divide the result by 2 (this gives the average base length).
- Multiply by the height.
🛎️ Example: How to Find the Area of a Trapezium?
- A trapezium has:
- Base 1 = 8 cm
- Base 2 = 12 cm
- Height = 6 cm
$$\text{Area} = \frac{8 + 12}{2} \times 6 = 10 \times 6 = 60 \text{ cm}^2$$
✅ So the area of this trapezium is 60 cm².
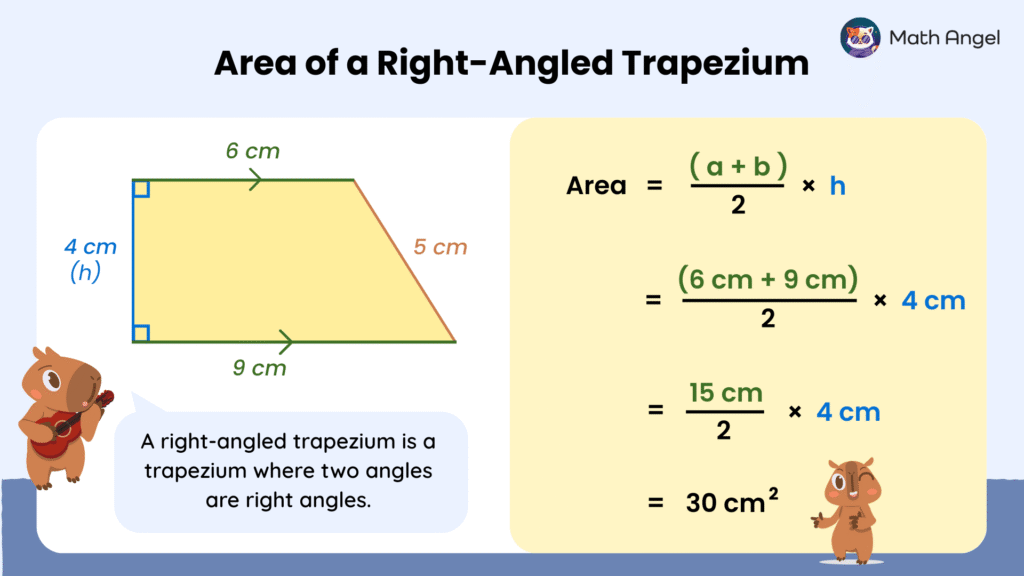
Finding the Area of a Right-Angled Trapezium
⏩️
🛎️ What is a Right-Angled Trapezium?
A right-angled trapezium has two right angles.
Good news! 🥳 The height is easy to spot: it’s the short side that meets both bases at right angles.
🛎️ Example: Finding the Area of a Right-Angled Trapezium
- Base 1 = 6 cm
- Base 2 = 9 cm
- Height = 4 cm
$$\text{Area} = \frac{6 + 9}{2} \times 4 = 15 \times 2 = 30 \text{ cm}^2$$
✅ So the area of this right-angled trapezium is 30 cm².
Finding the Area of a Isosceles Trapezium
⏩️
🛎️ What is a Isosceles Trapezium?
An isosceles trapezium has one pair of parallel sides and the other two sides are equal in length.
If you draw perpendicular lines from the ends of the top base to the bottom base, it splits the trapezium into:
- Two identical right-angled triangles (on each side)
- One rectangle (in the middle)
🛎️ Example: Finding the Height of a Isosceles Trapezium
- Top base = 5m
- Side parts = 2m each
- Bottom base = 2m + 5m + 2m = m
- Area of the trapezium = 21 m²
Calculation:
$$
\begin{aligned}
\frac{5 + 9}{2} \times h &= 21 \\[0.5em]
7 \times h &= 21 \\[0.5em]
h &= 3 \text{ cm}
\end{aligned}
$$
✅ So the height of this isosceles trapezium is 3 cm.
🍪 Quiz: Practice Calculating the Area of Trapeziums
🎩 Stuck on Area Calculation? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
