Volume and Surface Area of Pyramids, Cones, Spheres

🔮 What is a Pyramid?

A pyramid is a 3D shape with a flat base and triangular faces that meet at a single point (the apex).

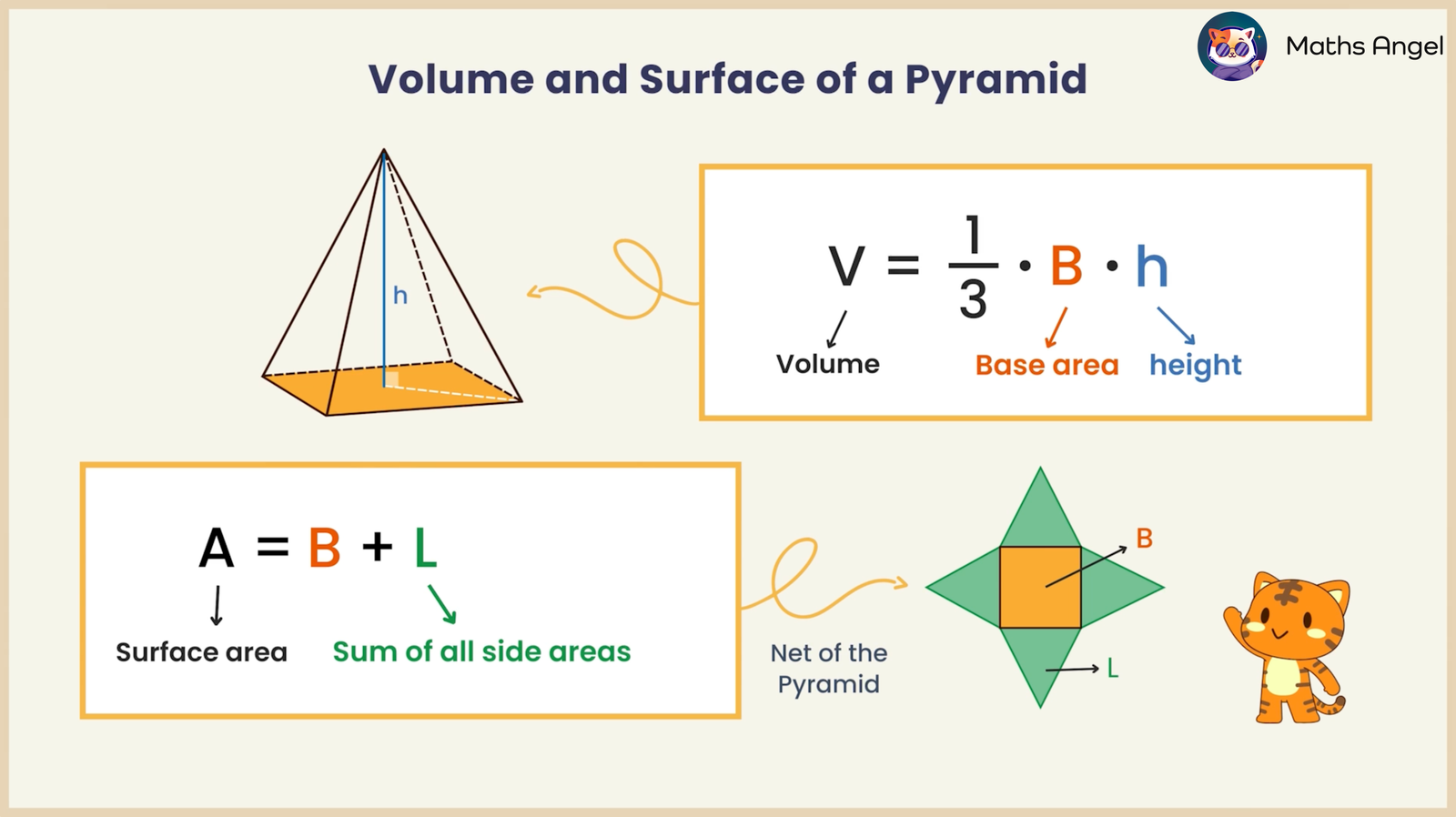
🌟 Volume of a Pyramid Formula

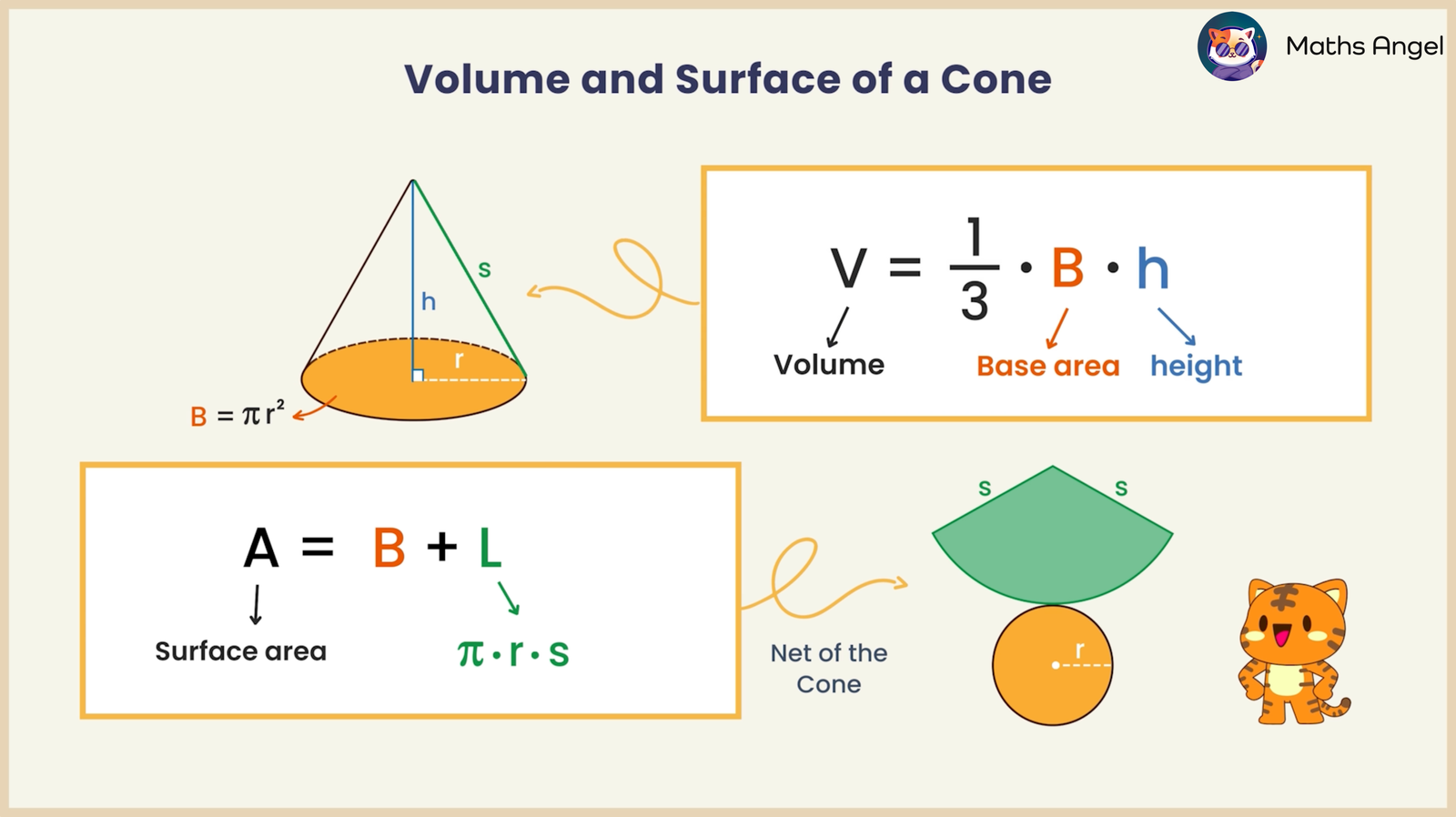
$$V = \frac{1}{3} \times B \times h$$

• $V$ = volume

• $B$ = base area

• $h$ = height

Be careful:

The height is the vertical distance from the base to the top. It always meets the base at a right angle (90°). Never use a sloping edge as the height.

🔮 What Is a Net?

A net is a flat pattern you can fold up to make a 3D shape. It shows all the faces of the solid. For a pyramid, the net shows the base and all the triangles that make up the sides. 

🌟 Surface Area of a Pyramid Formula

$$\text{Surface Area} = B + L$$

Where:

• $B$ = area of the base

• $L$ = total area of all the sloping side faces

Exam Tip:

The number of side faces on a pyramid always matches the number of sides on the base.

• Base has 3 sides (triangle) → 3 side faces
• Base has 4 sides (square/rectangle) → 4 side faces
• Base has 5 sides (pentagon) → 5 side faces
• …and so on

Double-check that you add up the area of every face. Don’t miss any when working out the surface area:)

Example:

A square-based pyramid with base length $10,\text{cm}$, height $12,\text{cm}$, and slant height $13,\text{cm}$. Fins its volume and surface area.

🌟 Finding the Volume of the Pyramid:

Use the formula:

$$V = \frac{1}{3} \times B \times h$$

Steps:

• Find the area of the base: $B = 10\text{ cm} \times 10\text{ cm} = 100\text{ cm}^2$

• Use the vertical height $h = 12\text{ cm}$

$$V = \frac{1}{3} \times 100 \text{ cm}^2 \times 12 \text{ cm} = 400\text{ cm}^3$$

So, volume is $400 \text{ cm}^3$.

🌟 How to Find the Surface Area of the Pyramid:

Use the formula:

$$A=B+L$$

where $B$ is the area of the base, and $L$ is the total area of all 4 triangle faces.

Steps:

1. Base area: $10 \text{ cm} \times 10 \text{ cm} = 100 \text{ cm}^2$

2. Each triangle face: $\frac{1}{2} \times 10 \text{ cm} \times 13\text{ cm} = 65\text{ cm}^2$

3. There are 4 triangle faces, so $L = 4 \times 65\text{ cm}^2 = 260\text{ cm}^2$

4. Add together: $100\text{ cm}^2 + 260\text{ cm}^2 = 360\text{ cm}^2$

So, surface area is $ 360 \text{ cm}^2$.