Volume and Surface Area of Pyramids, Cones, Spheres
🎬 Video Tutorial
Volume of a Pyramid (Formula) (0:01)
🔮 What is a Pyramid?
A pyramid is a 3D shape with a flat base and triangular faces that meet at a single point (the apex).
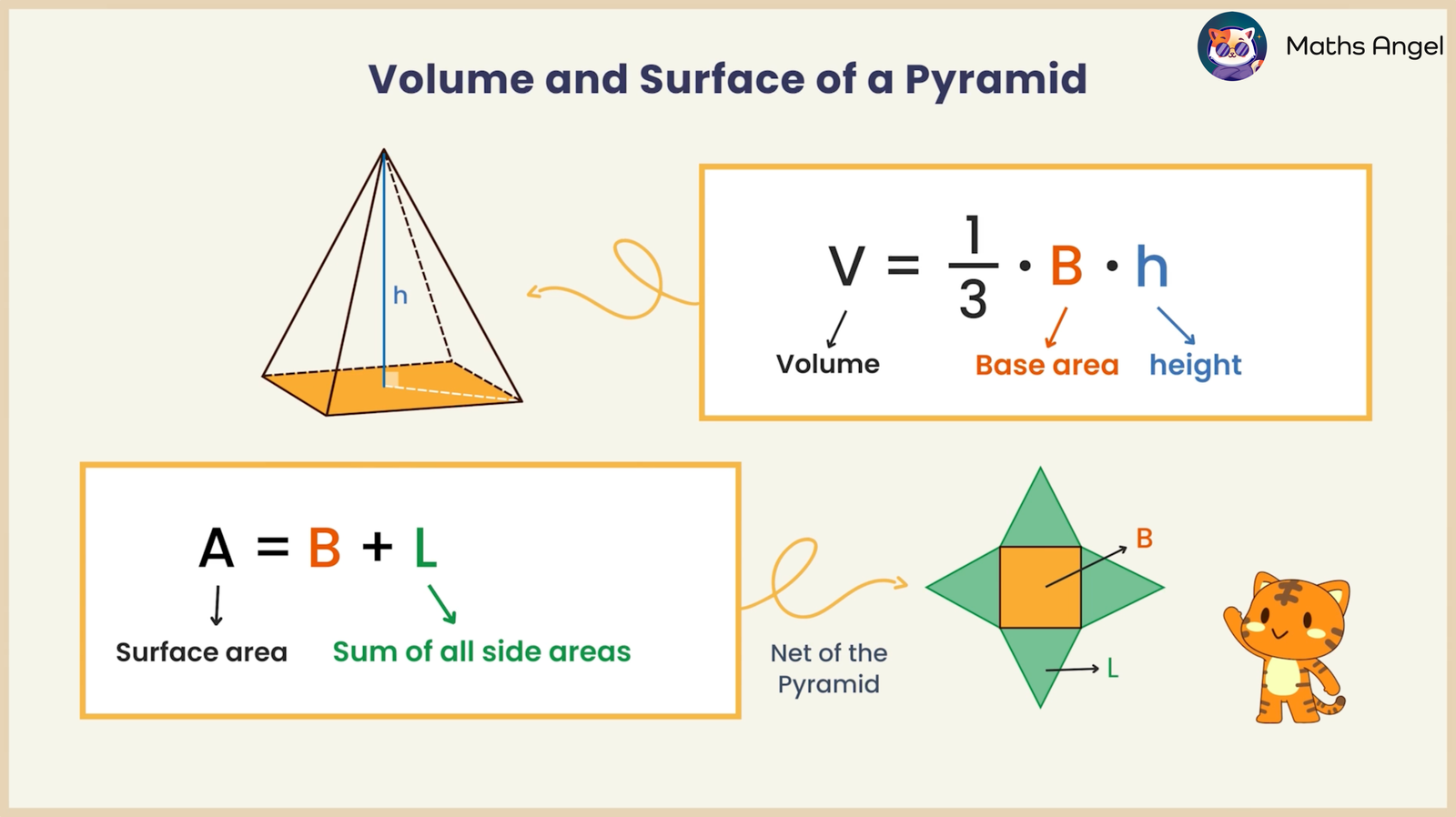
🌟 Volume of a Pyramid Formula
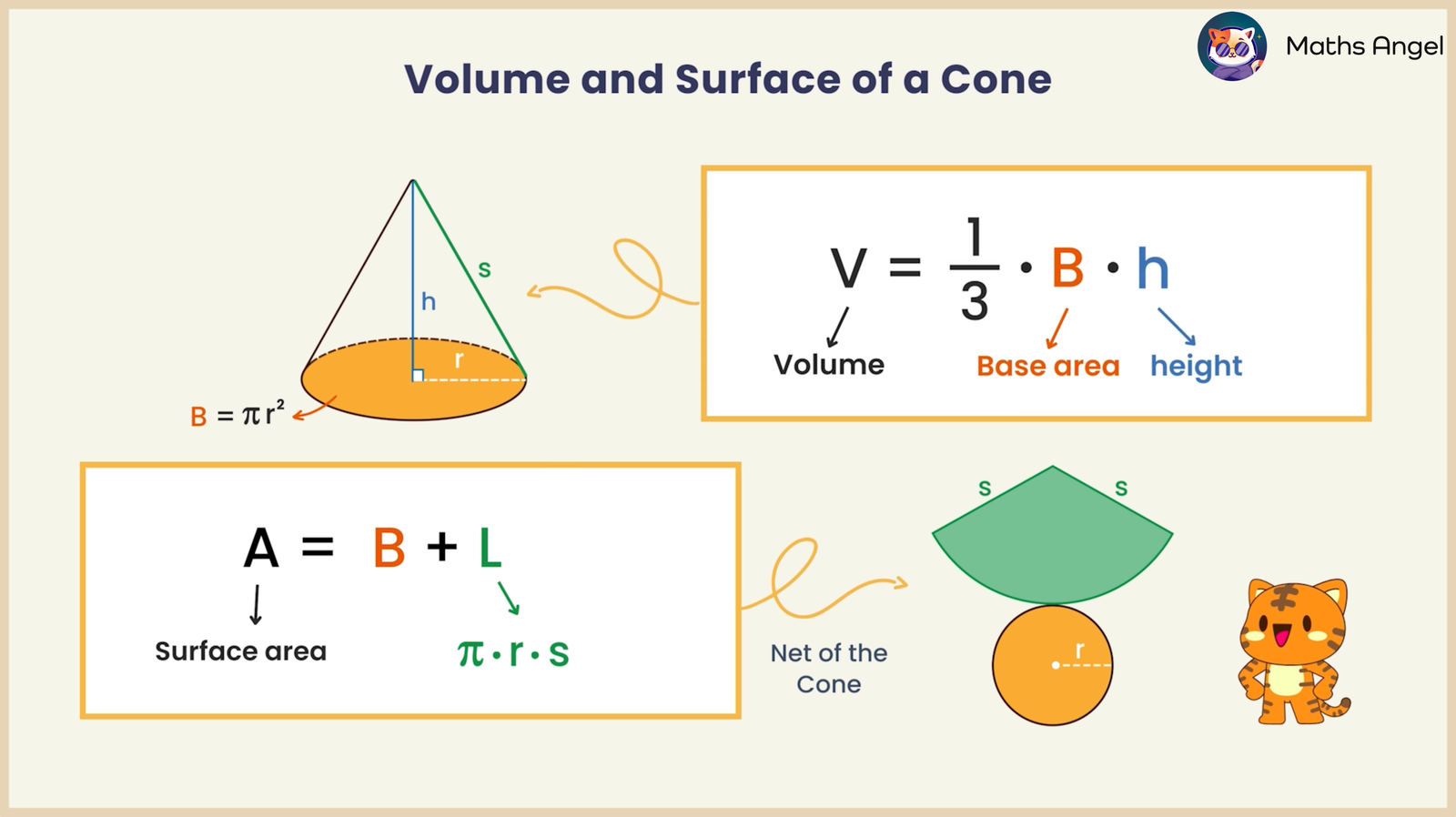
$$V = \frac{1}{3} \times B \times h$$
$V$ = volume
$B$ = base area
$h$ = height
Be careful:
The height is the vertical distance from the base to the top. It always meets the base at a right angle (90°). Never use a sloping edge as the height.
Surface Area of a Pyramid (Formula) (0:37)
🔮 What Is a Net?
A net is a flat pattern you can fold up to make a 3D shape. It shows all the faces of the solid. For a pyramid, the net shows the base and all the triangles that make up the sides.
🌟 Surface Area of a Pyramid Formula
$$\text{Surface Area} = B + L$$
Where:
$B$ = area of the base
$L$ = total area of all the sloping side faces
Exam Tip:
The number of side faces on a pyramid always matches the number of sides on the base.
- Base has 3 sides (triangle) → 3 side faces
- Base has 4 sides (square/rectangle) → 4 side faces
- Base has 5 sides (pentagon) → 5 side faces
- …and so on
Double-check that you add up the area of every face. Don’t miss any when working out the surface area:)
Volume and Surface Area of a Pyramid (Example) (1:00)
Example:
A square-based pyramid with base length $10,\text{cm}$, height $12,\text{cm}$, and slant height $13,\text{cm}$. Fins its volume and surface area.
🌟 Finding the Volume of the Pyramid:
Use the formula:
$$V = \frac{1}{3} \times B \times h$$
Steps:
Find the area of the base: $B = 10\text{ cm} \times 10\text{ cm} = 100\text{ cm}^2$
Use the vertical height $h = 12\text{ cm}$
$$V = \frac{1}{3} \times 100 \text{ cm}^2 \times 12 \text{ cm} = 400\text{ cm}^3$$
So, volume is $400 \text{ cm}^3$.
🌟 How to Find the Surface Area of the Pyramid:
Use the formula:
$$A=B+L$$
where $B$ is the area of the base, and $L$ is the total area of all 4 triangle faces.
Steps:
Base area: $10 \text{ cm} \times 10 \text{ cm} = 100 \text{ cm}^2$
Each triangle face: $\frac{1}{2} \times 10 \text{ cm} \times 13\text{ cm} = 65\text{ cm}^2$
There are 4 triangle faces, so $L = 4 \times 65\text{ cm}^2 = 260\text{ cm}^2$
Add together: $100\text{ cm}^2 + 260\text{ cm}^2 = 360\text{ cm}^2$
So, surface area is $ 360 \text{ cm}^2$.
📂 Revision Cards


🍪 Quiz Time - Practice Now!
Membership Required
You must be a member of Math Angel Plus or Math Angel Unlimited to view this content.
🎩 Stuck on Volume or Surface Problems? Try Our AI
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

