Solids and Units of Volume

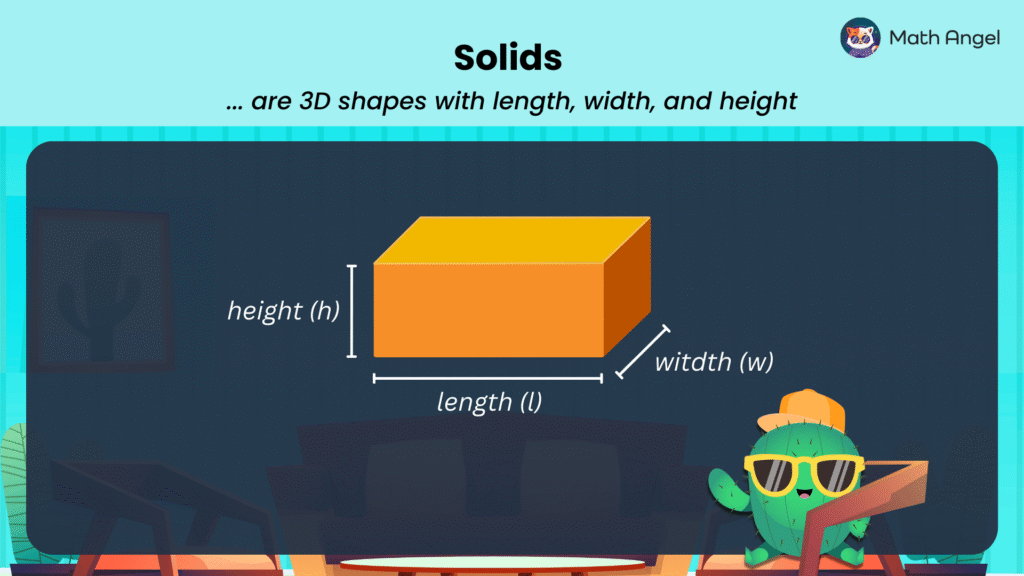
🌟 Solids are 3D shapes that have length, width, and height.

• Length ($l$): How long the shape is.

• Width ($w$): How wide the shape is.

• Height ($h$): How tall the shape is.

For example, a cuboid is a solid because it has three dimensions: length, width, and height.

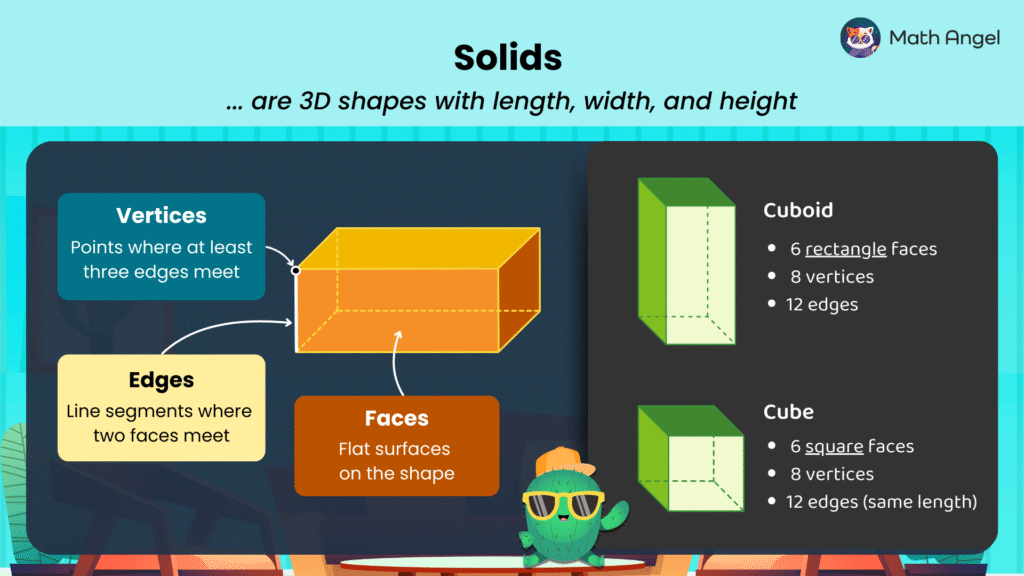
🌟 3D shapes with flat surfaces have vertices, edges, and faces.

• Vertices: Points where at least three edges meet.

• Edges: Straight lines where two faces meet.

• Faces: Flat surfaces on the shape.

🟧 Cuboid:

A cuboid is a 3D shape with six rectangular faces. It has:

• 6 rectangle faces
• 8 vertices
• 12 edges

🟧 Cube:

A cube is a special cuboid where all the faces are squares and all edges are equal. It has:

• 6 square faces (all the same size)
• 8 vertices
• 12 edges (all the same length)

🌟 Definition of Volume

Volume is the amount of space a solid shape occupies.

🌟 Units of Volume

Volume is measured in cubic units (like $\text{cm}^3$).

🌟 Example of Volume

If a solid can hold exactly $27$ unit cubes, where each cube is $1 \text{ cm}^3$ (with $1\text{ cm}$ edge length), then the volume of the solid is $27 \text{ cm}^3$.

Units of volume measure how much space something takes up.

In math, we use different units depending on the size of the object.

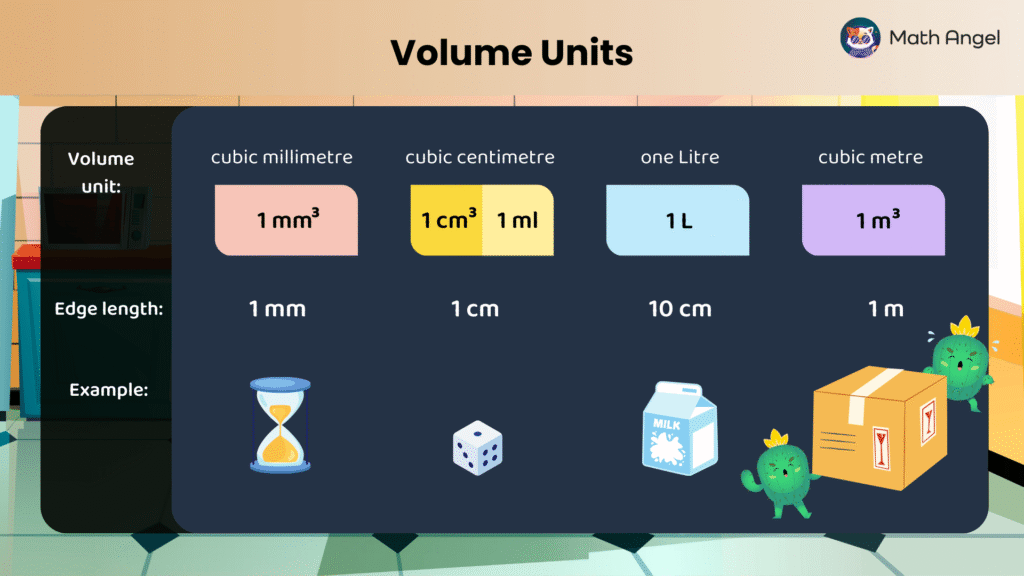
• Cubic millimeter:

  • $\textcolor{Violet}{1 \text{ mm} \times 1 \text{ mm} \times 1 \text{ mm} = 1 \text{ mm}^3}$
  • $1 \text{ mm}^3$ is the space inside a cube with edge length $1 \text{ mm}$
  • Example: A tiny grain of sand is about $1 \text{ mm}^3$

• Cubic centimeter and milliliter:

  • $\textcolor{Violet}{1 \text{ cm} \times 1 \text{ cm} \times 1 \text{ cm} = 1 \text{ cm}^3}$
  • $1 \text{ cm}^3$ is the space inside a cube with edge length $1 \text{ cm}$
  • Example: A sugar cube or a small dice has a volume of about $1 \text{ cm}^3$
  • $1 \text{ cm}^3$ is exactly the same as $1 \text{ ml}$
  • Milliliters $\text{ml}$ are often used for measuring liquids like drinks

• Liter:

  • $\textcolor{Violet}{10 \text{ cm} \times 10 \text{ cm} \times 10 \text{ cm} = 1000 \text{ cm}^3 = 1 \text{ L}}$
  • $1 \text{ L}$ is the space inside a cube with edge length $10 \text{ cm}$
  • Example: A carton of milk is usually $1 \text{ L}$

• Cubic meter:

  • $\textcolor{Violet}{1 \text{ m} \times 1 \text{ m} \times 1 \text{ m} = 1 \text{ m}^3}$
  • $1 \text{ m}^3$ is the space inside a cube with edge length $1 \text{ m}$
  • Example: A large packing box or a washing machine is about $1 \text{ m}^3$

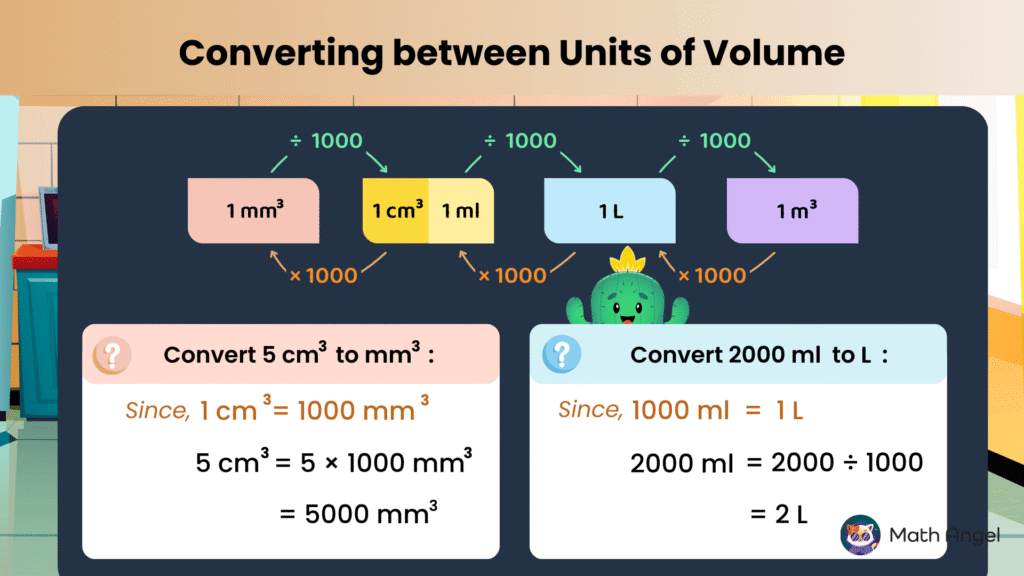
Here’s how the main volume units are connected:

• $1 \text{ cm}^3 = 1 \text{ ml}$
• $1 \text{ L} = 1000 \text{ ml} = 1000 \text{ cm}^3$
• $1 \text{ m}^3 = 1000 \text{ L}$

🌟 To convert to a bigger unit, divide by 1000.

🌟 To convert to a smaller unit, multiply by 1000.

🔎 Example 1: Convert $ 5 \text{ cm}^3 \text{ to} \text{ mm}^3$

• Since $1 \text{ cm}^3 = 1000 \text{ mm}^3$
• $5 \text{ cm}^3 = 5 \times 1000 \text{ mm}^3 = 5000 \text{ mm}^3$

🔎 Example 2: Convert $ 2000 \text{ ml}^3 \text{ to} \text{ L}$

• Since $1000 \text{ ml} = 1 \text{ L}$
• $2000 \text{ ml} = 2000 \div 1000 = 2 \text{ L}$