Secondary School | Grade 7-12
Learn Math Faster
& Easier Than Ever
You learn in minutes what normally takes weeks with our structured lessons and advanced AI.


Structured
Learn any topic under 4 minutes with a clear, easy-to-follow path.
Creative
No walls of text. Fun, visual learning that just makes sense.
Comprehensive
Secondary math curriculum, all under one platform, no endless searching.
Learn Faster with
Bite-Sized Videos
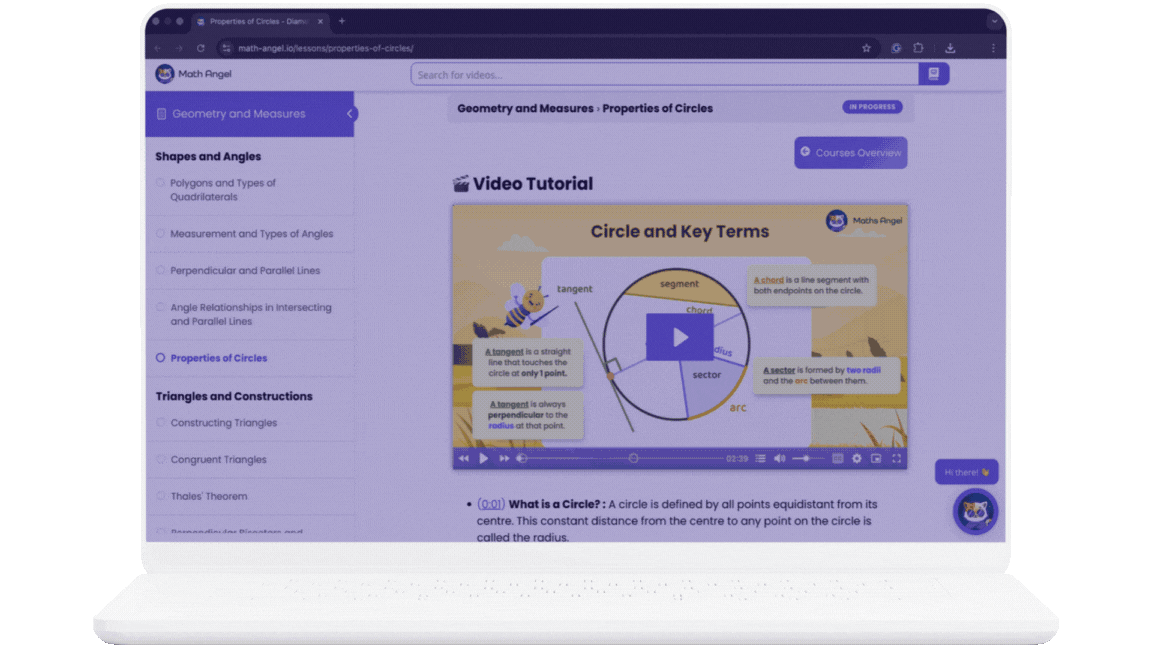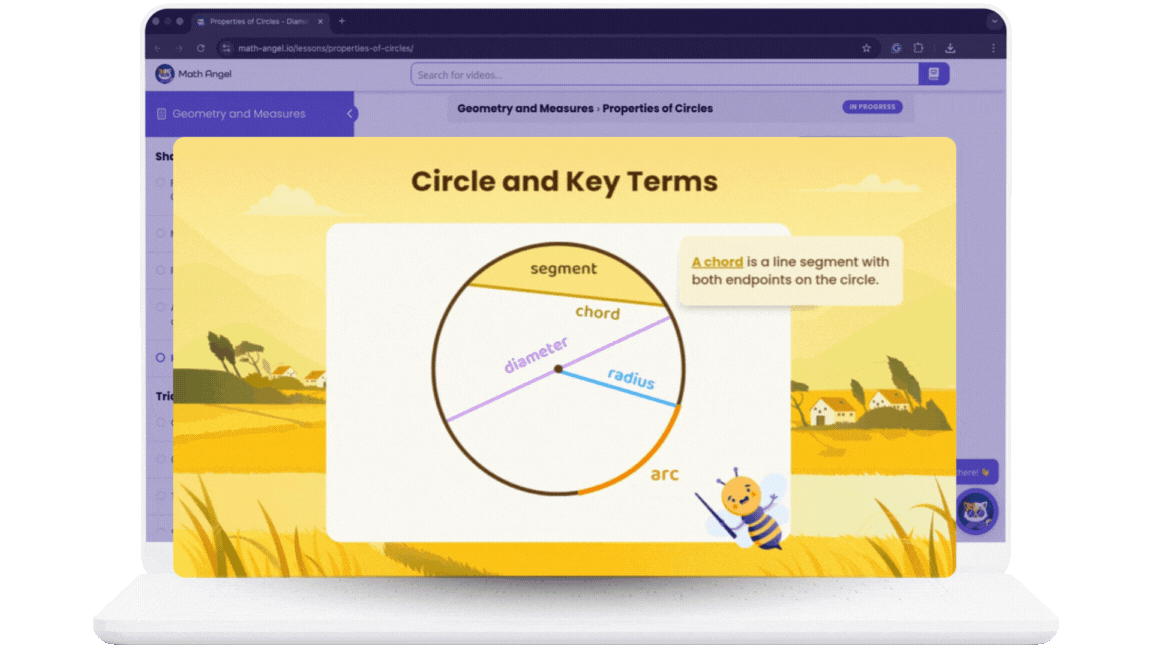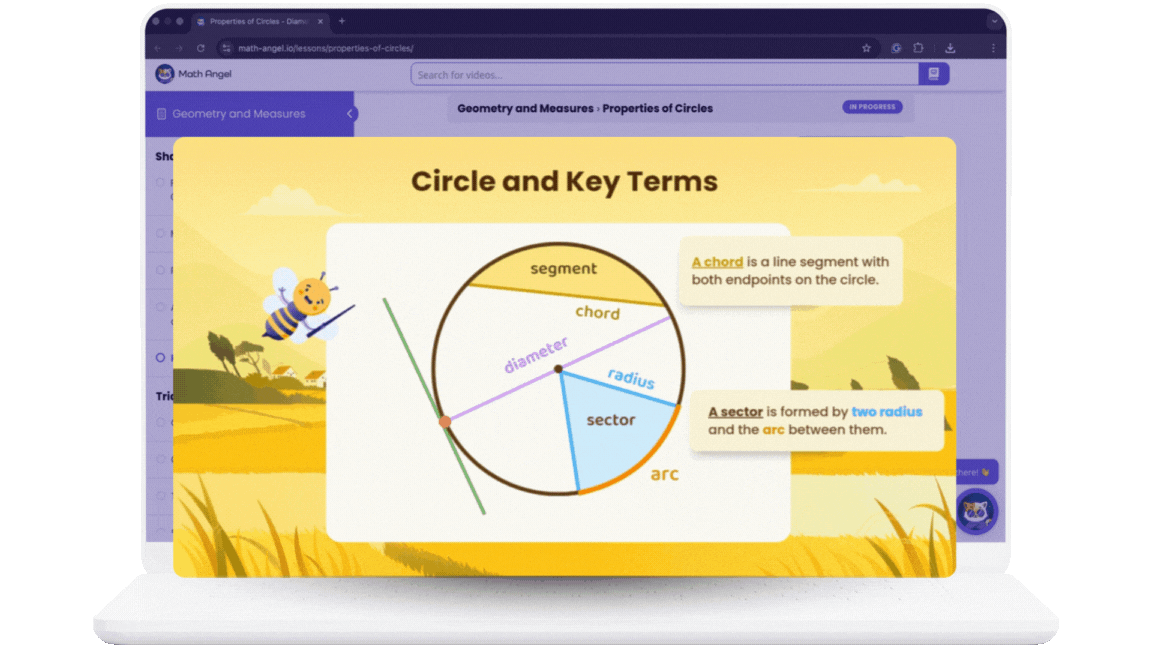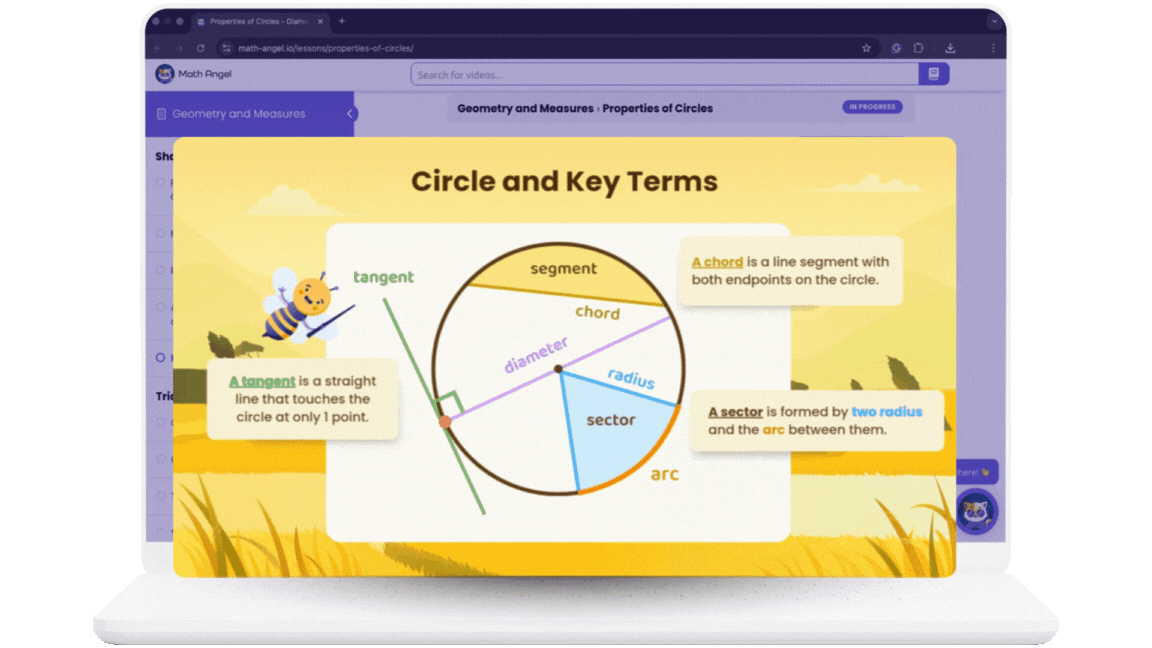
Practice smarter with
Exam-Style Questions

Instant Feedback
Know exactly where you went wrong and get explanations to level up your learning.
Smart Progression
Start easy, end strong. Build your skills step by step and gain real confidence.
Track Your Scores
Compare with students worldwide. Perfect for group and self-paced learning.
Stuck on a math problem?
Your 24/7 AI Math Solver
Stuck with homework?
Your 24/7 AI Math Solver
Quick Help Anytime
Judgment-Free
Multilingual
Step-By-Step Guidance
Photo Recognition
Fill Knowledge Gaps
Quick Help Anytime
Judgment-Free
Multilingual
Step-By-Step Guidance
Photo Recognition
Fill Knowledge Gaps
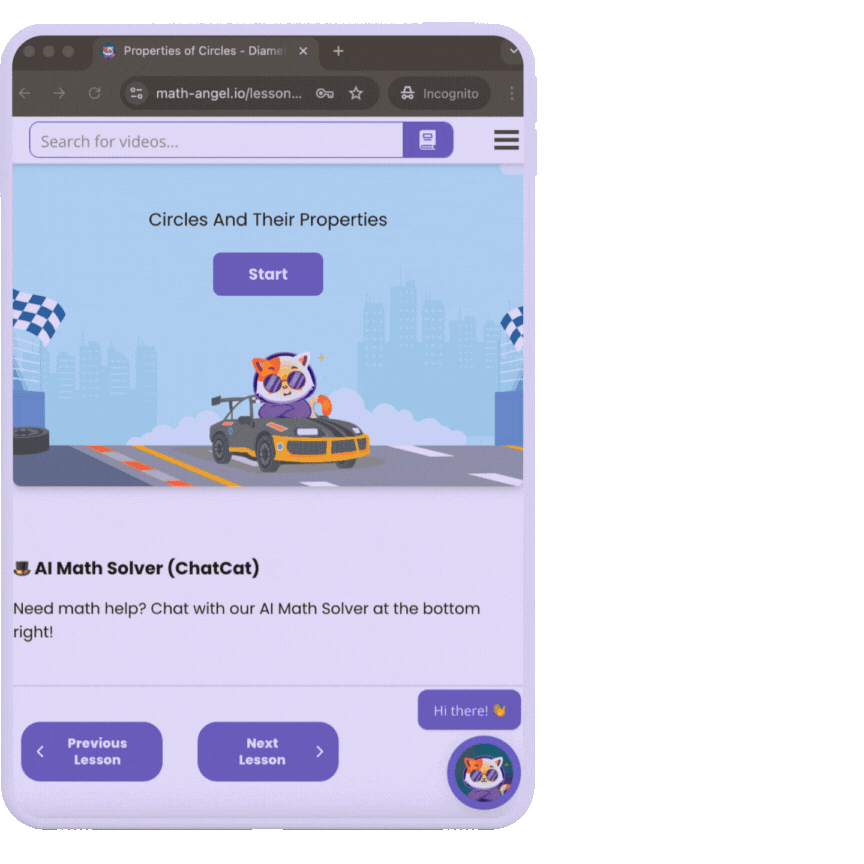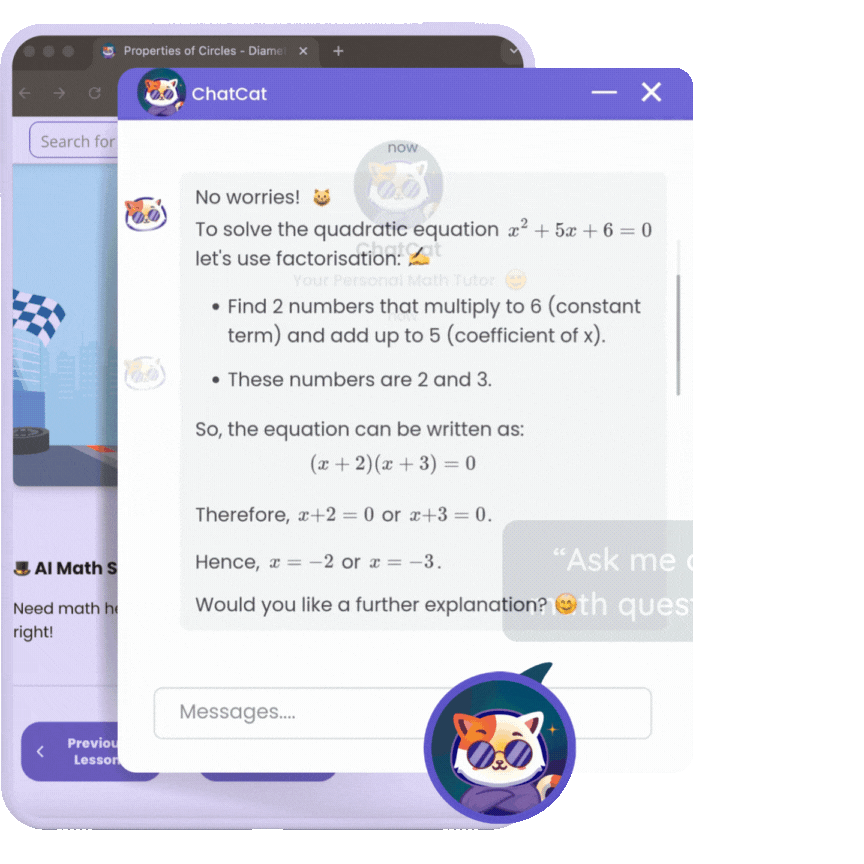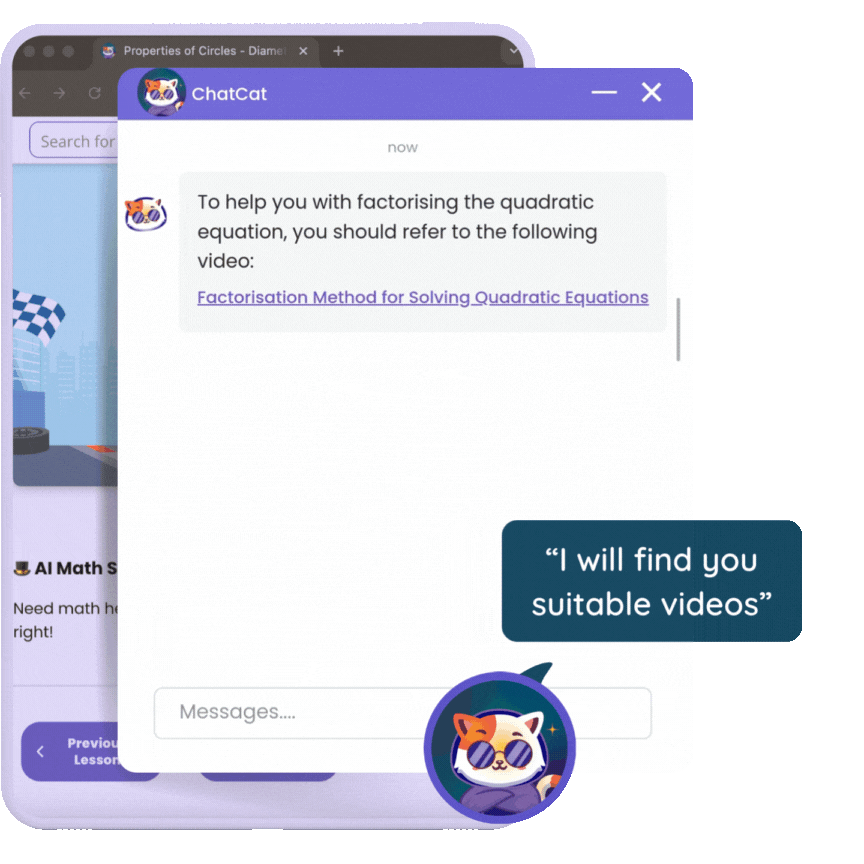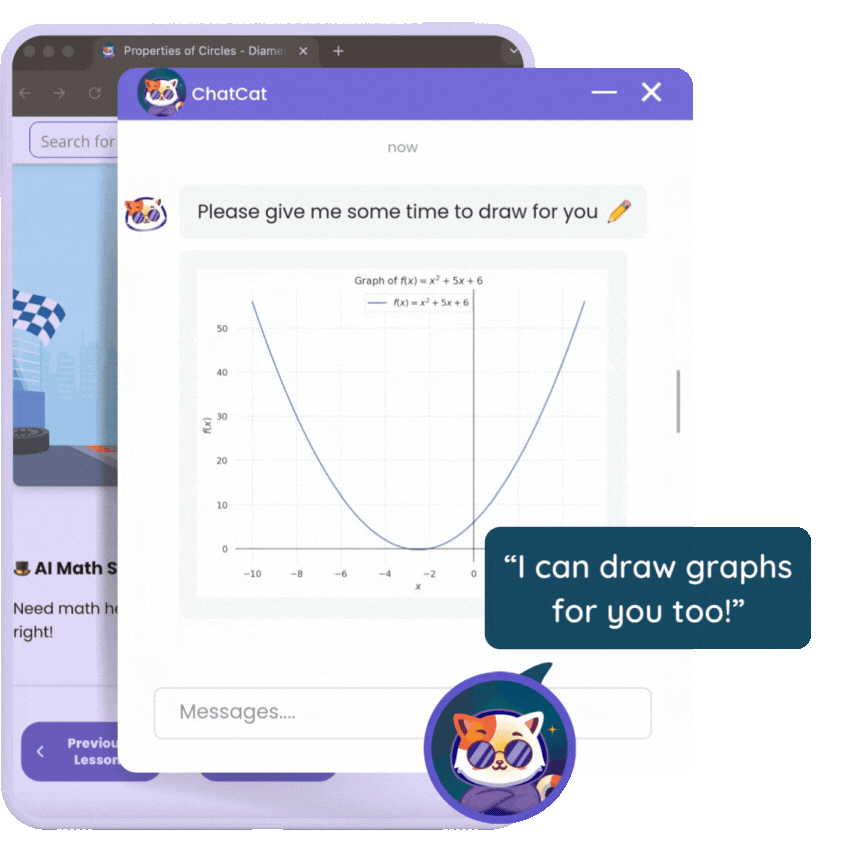
Less effort & better results
Using Math Angel
Watch 1 video, review with 3 flashcards, practice with 6 exercises, and ask AI for any questions.
Over 10,000 students, parents, and teachers are using Math Angel
Will you be next?

★★★★★
Grade 7 Student
With Math Angel, I like to pre-learn before math class, so I walk in feeling confident. I can also catch up at home if I miss anything.

★★★★★
Grade 9 Student
If I’m stuck on a math problem, I just take a picture and ask the AI solver. It’s so cool, it explains everything until I get it!

★★★★★
Math Tutor
With Math Angel, I can focus on teaching instead of creating materials from scratch. I also enjoy using AI to generate activities and examples.

★★★★★
Parent
It’s been years since I’ve done maths beyond the basics, so helping my son felt daunting. Thanks to Math Angel, I can brush up my knowledge too!

★★★★★
Math Teacher
Math Angel is now my go-to for lesson prep, as it saves me so much time. My students stay focused and engaged when I play the videos in class.











