Powers and Indices
Table Of Contents
🎬 Math Angel Video: Powers Definition, Notation, Examples
Introduction to Powers
⏩️
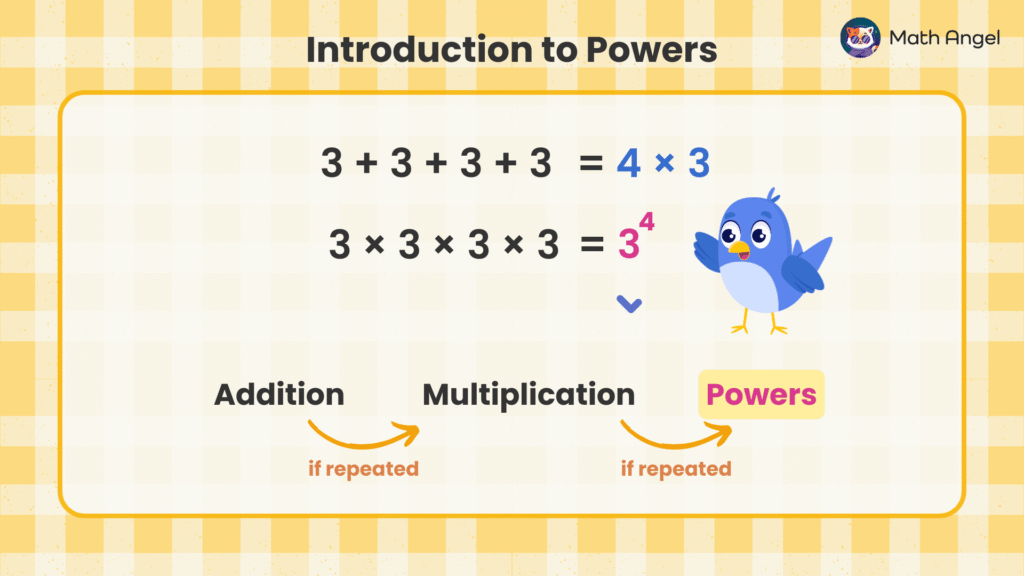
🛎️ Repeated Addition → Multiplication
If we add the same number again and again, we can write it as multiplication.
Example:
$$3 + 3 + 3 + 3 = 4 \times 3$$
🛎️ Repeated Multiplication → Powers
If we multiply the same number again and again, we can write it as a power.
Example:
$$3 \times 3 \times 3 \times 3 = 3^4$$
What are Powers in Math?
⏩️
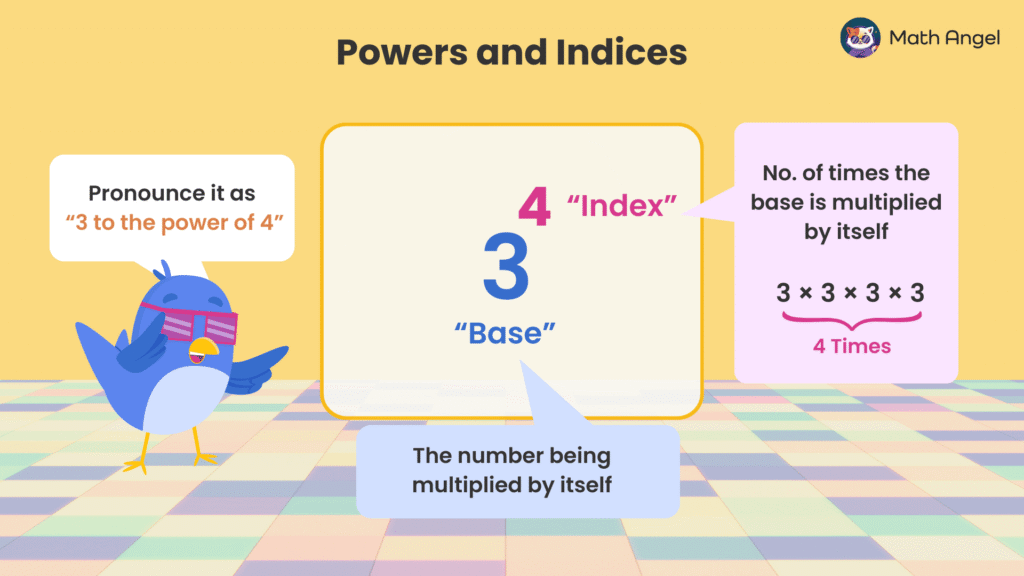
🛎️ Definition and Notation of a Power:
A power is a way of writing repeated multiplication of the same number.
They help express large and small numbers efficiently.
In general, a power is written as: $$ \large a^n $$
where:
- $ a $ is the base. The base is the number being multiplied.
- $ n $ is the index (exponent). The index (exponent) tells us how many times the base is multiplied by itself.
🛎️ Example of a Power in Math:
$$ 3^4 = 3 \times 3 \times 3 \times 3 $$
- Here, 3 is the base.
- 4 is the index, meaning 3 is multiplied by itself 4 times.
- This is pronounced as “3 to the power of 4”.
What are Key Properties of Powers?
⏩️
Understanding the following properties will help you develop a strong grasp of exponents and indices.
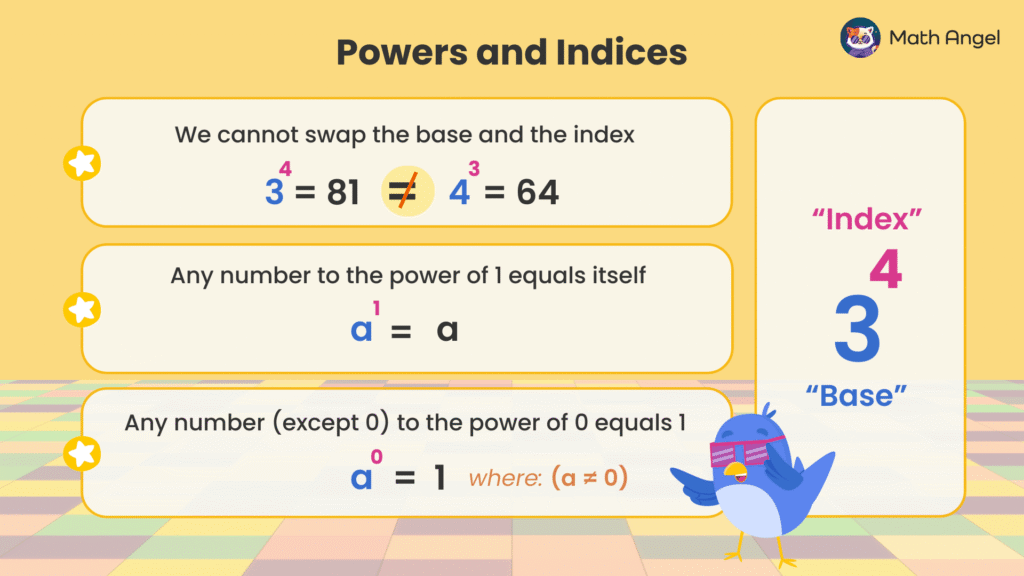
The Base and Exponent Cannot Be Swapped.
$$ \text{For example, } 3^4 \neq 4^3 $$
Any Number to the Power of 1 Equals Itself.
$$ a^1 = a $$
Any Number (Except 0) to the Power of 0 Equals 1.
$$ a^0 = 1 \quad \text{where } a \neq 0 $$
What are Square Numbers and Cube Numbers?
⏩️
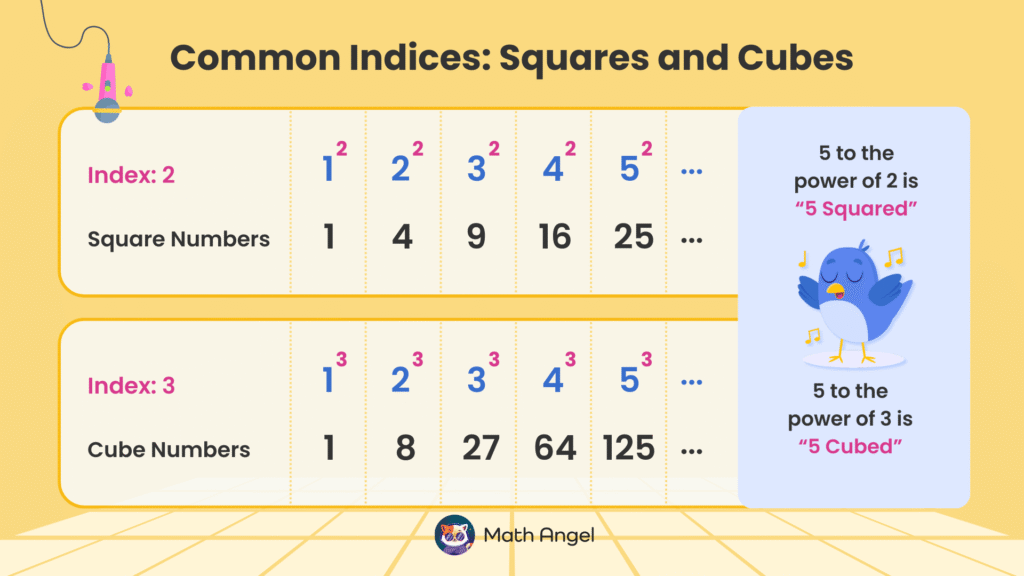
Two of the most common powers are squares (index 2) and cubes (index 3).
🛎️ Square Numbers:
- A square number is a number that results from multiplying a whole number by itself.
$$ n^2 = n \times n $$
- Common Square Numbers:
$$ 1^2 = 1, \quad 2^2 = 4, \quad 3^2 = 9, \quad 4^2 = 16, \quad 5^2 = 25 $$
🛎️ Cube Numbers:
- A cube number is a number that results from multiplying a whole number by itself three times.
$$ n^3 = n \times n \times n $$
- Common Cube Numbers:
$$ 1^3 = 1, \quad 2^3 = 8, \quad 3^3 = 27, \quad 4^3 = 64, \quad 5^3 = 125 $$
How to Use Exponents to Simplify Expressions?

⏩️
When multiplying the same number multiple times, you can use exponents (indices) to write the expression in a simplified form.
For example:
$$ 4 \times 3 \times 3 \times 4 \times 4 = ? $$
We can group the same factors using the commutative and associative laws:
$$ (4 \times 4 \times 4) \times (3 \times 3) $$
Since each base is repeated, we can write it using exponents:
$$ 4^3 \times 3^2 $$
By using exponents for repeated multiplication, you make expressions easier to read, write, and work with.
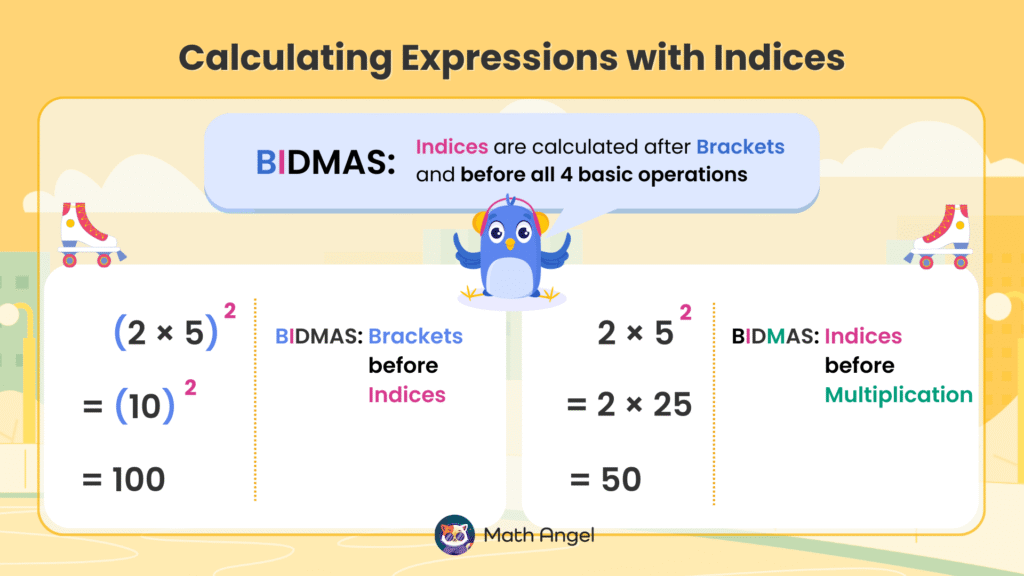
How to Apply BIDMAS with Powers (Indices)?
⏩️
In BIDMAS (Brackets, Indices, Division, Multiplication, Addition, Subtraction),
indices (exponents) are calculated after brackets but before all basic operations.
🛎️ Example 1: Brackets Before Indices
When an expression has brackets, evaluate the brackets first:
$$ (2 \times 5)^2 = ? $$
- Step 1: Solve inside the brackets:
$$ (10)^2 $$
- Step 2: Apply the exponent:
$$ 100 $$
🛎️ Example 2: Indices Before Multiplication
If there are no brackets around the multiplication, apply the exponent first:
$$ 2 \times 5^2 = ? $$
- Step 1: Evaluate the exponent first:
$$ 2 \times 25 $$
- Step 2: Perform the multiplication:
$$ 50 $$
🍪 Quiz: Practice with Indices and Exponents
🎩 Struggling with Powers? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

