The nth Root and Fractional Indices
Table Of Contents
🎬 Math Angel Video: nth Roots and Simplifying Indices
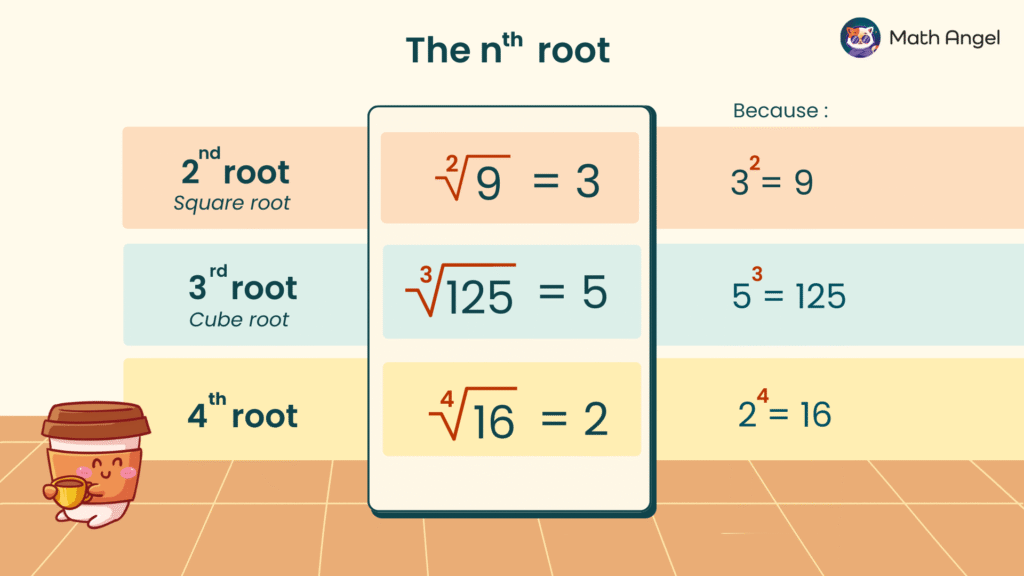
What is the nth Root?
⏩️
🛎️ Definition of nth Root:
The nth root of a number is the value that, when raised to the power of $ n $, gives the original number. It is written as:
$$ \Large \sqrt[n]{x} $$
🛎️ Examples of nth Root:
- Square root ($ 2^{nd} $ root):
$$ \sqrt{9} = 3 \quad \text{(Since } 3^2 = 9 \text{)} $$ - Cube root ($ 3^{rd} $ root):
$$ \sqrt[3]{125} = 5 \quad \text{(Since } 5^3 = 125 \text{)} $$ - Fourth root ($ 4^{th} $ root):
$$\sqrt[4]{16} = 2 \quad \text{(since } 2^4 = 16\text{)}$$
What is the nth Root Rule?
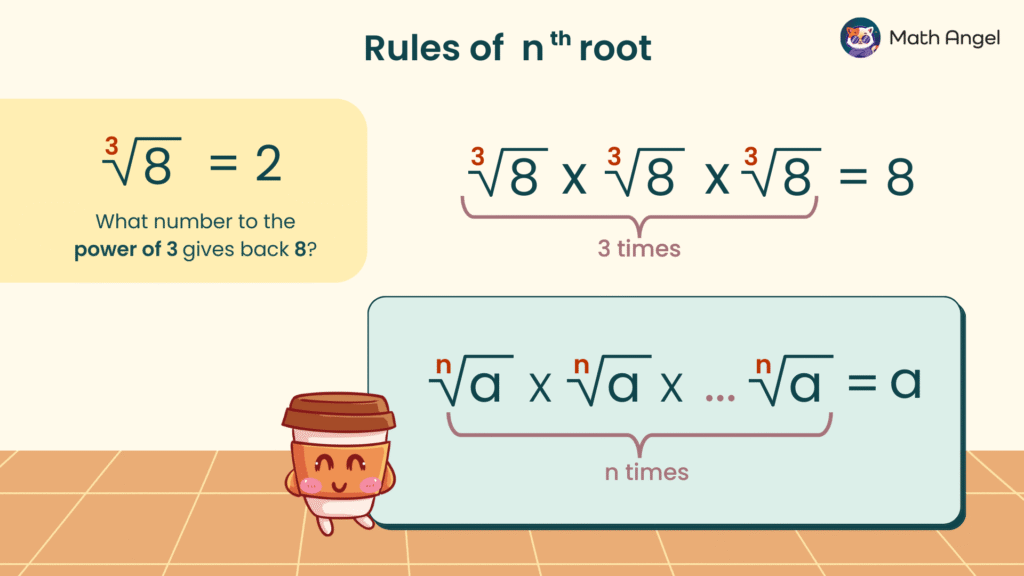
⏩️
🛎️ Definition of the nth Root Rule
The nth root rules tells us, if you multiply the nth root of a number exactly n times, you get back the original number.
$$
\Large \underbrace{\sqrt[n]{a} \times \sqrt[n]{a} \times \cdots \times \sqrt[n]{a}}_{\text{n times}} = a
$$
🛎️ Examples of Using the nth Root Rule
- Example 1: If you multiply $ \sqrt[3]{8}$ three times, you get 8.
$$ \sqrt[3]{8} \times \sqrt[3]{8} \times \sqrt[3]{8} = 8 $$
- Example 2: If you multiply $ \sqrt[4]{16}$ four times, you get 16.
$$ \sqrt[4]{16} \times \sqrt[4]{16} \times \sqrt[4]{16} \times \sqrt[4]{16} = 16 $$
What is the Fractional Exponent Rule?

⏩️
🛎️ Definition of the Fractional Exponent Rule
The Fractional Exponent Rule connects exponents and roots:
$$ \Large a^{\frac{1}{n}} = \sqrt[n]{a} $$
It tells us that taking the nth root of a number is the same as raising it to the power of $ \frac{1}{n}$.
🛎️ Example:
$$
\sqrt[3]{8} = 8^{\frac{1}{3}}
$$
- If we multiply $\sqrt[3]{8}$ by itself three times, we get:
$$
\sqrt[3]{8} \times \sqrt[3]{8} \times \sqrt[3]{8} = 8
$$
- If we multiply $8^{\frac{1}{3}}$ by itself three times, we also get:
$$
8^{\frac{1}{3}} \times 8^{\frac{1}{3}} \times 8^{\frac{1}{3}} = 8^{1} = 8
$$
- Therefore,
$$
8^{\frac{1}{3}} = \sqrt[3]{8} = 2
$$
Practice: Fractional Index and Cube Root
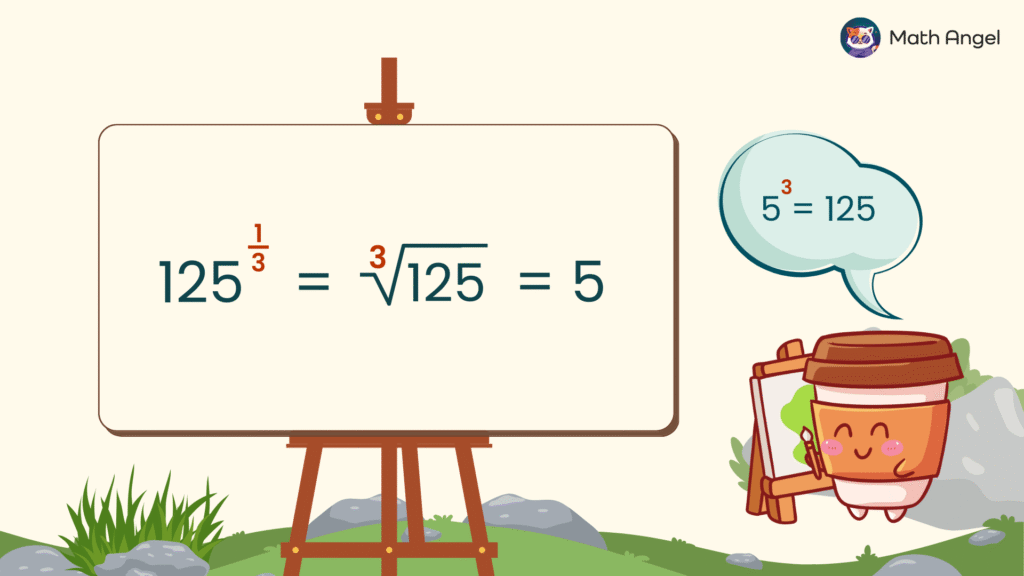
⏩️
🛎 Practice:
$$
125^{\frac{1}{3}} = ?
$$
If we multiply $125^{\frac{1}{3}}$ by itself three times, we get:
$$
125^{\frac{1}{3}} \times 125^{\frac{1}{3}} \times 125^{\frac{1}{3}} = 125^{1} = 125
$$
This means $125^{\frac{1}{3}}$ is the cube root of 125:
$$ 125^{\frac{1}{3}} = \sqrt[3]{125} = 5 $$
How to Simplify Fractional Indices?

⏩️
🛎️ The Fractional Exponent Rule:
The fractional index rule states that an exponent in the form of a fraction can be rewritten using roots:
$$ \Large a^{\frac{m}{n}} = \left( \sqrt[n]{a} \right)^m $$
This means:
- The denominator ($ n $) represents the nth root.
- The numerator ($ m $) represents the power applied after taking the root.
🛎️ Example of Simplifying Fractional Index:
$$ 125^{\frac{2}{3}} = ? $$
- Rewrite the fractional exponent:
$$ 125^{\frac{2}{3}} = 125^{\frac{1}{3} \times 2} = \left(125^{\frac{1}{3}}\right)^2 $$ - Find the cube root of 125:
$$ 125^{\frac{1}{3}} = \sqrt[3]{125} = 5 $$ - Square the result:
$$ 5^2 = 25 $$ - Thus:
$$ 125^{\frac{2}{3}} = 25 $$
Practice: Simplify Fractional Indices

⏩️
🛎 Example:
$$
16^{\frac{3}{4}} = ?
$$
- Rewrite the fractional exponent:
$$ 16^{\frac{3}{4}} = 16^{\frac{1}{4} \times 3} = \left(16^{\frac{1}{4}}\right)^3 $$ - Find the 4th root of 16:
$$ 16^{\frac{1}{4}} = \sqrt[4]{16} = 2 $$ - Cube the result:
$$ 2^3 = 8 $$ - Thus:
$$ 16^{\frac{3}{4}}= 8$$
🍪 Quiz: Practice Roots and Fractional Exponents
🎩 Stuck on Roots or Indices? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

