Units and Fractions

Previous Lesson
Next Lesson

Multiplying Fractions

Units and Fractions Multiplying Fractions

🎬 Video Tutorial

  • (0:01) Basic Fraction Multiplication: To multiply two fractions, multiply their numerators and denominators. Simplify the result if possible.
  • (0:23) Cross-Cancelling for Simplification: Before multiplying, look for common factors between any numerator and denominator to reduce fractions early, making calculations easier.
  • (1:30) Multiplying Fractions by Whole Numbers: Rewrite the whole number as a fraction over 1, then multiply as usual, using cross-cancelling to simplify if possible.
  • (2:18) Multiplying Mixed Fractions: Convert mixed fractions to improper fractions before multiplying to avoid errors, as mixed fractions represent addition, not multiplication.

📂 Revision Cards

Explanation of how to multiply fractions using the general method and cross-cancelling method, showing steps and simplification.
Cross-cancelling method for multiplying fractions 1/2 and 3/5, showing the simplified result as 3/10.
Multiplication of 88 piano keys by the fraction 13/22 to find the number of black keys, resulting in 52.
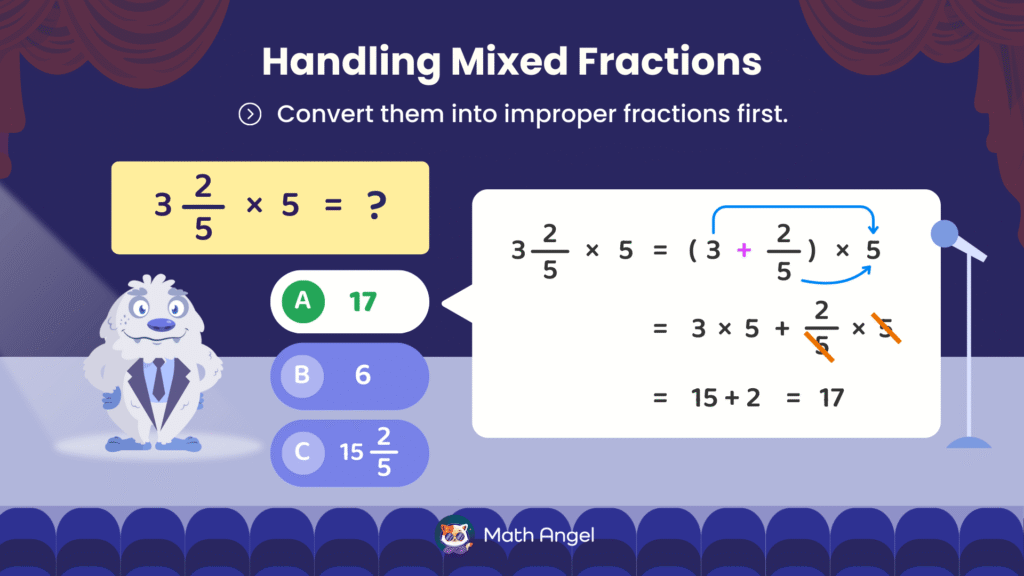
Explanation of handling mixed fractions by converting them into improper fractions, with the correct answer highlighted as 17.

💬 ChatCat (AI Math Tutor)

Courses Overview
Previous Lesson
Back to Course
Next Lesson