Medians and Centroid of a Triangle
Table Of Contents
🎬 Math Angel Video: Medians and Centroid Explained
What is Median of a Triangle?
⏩️
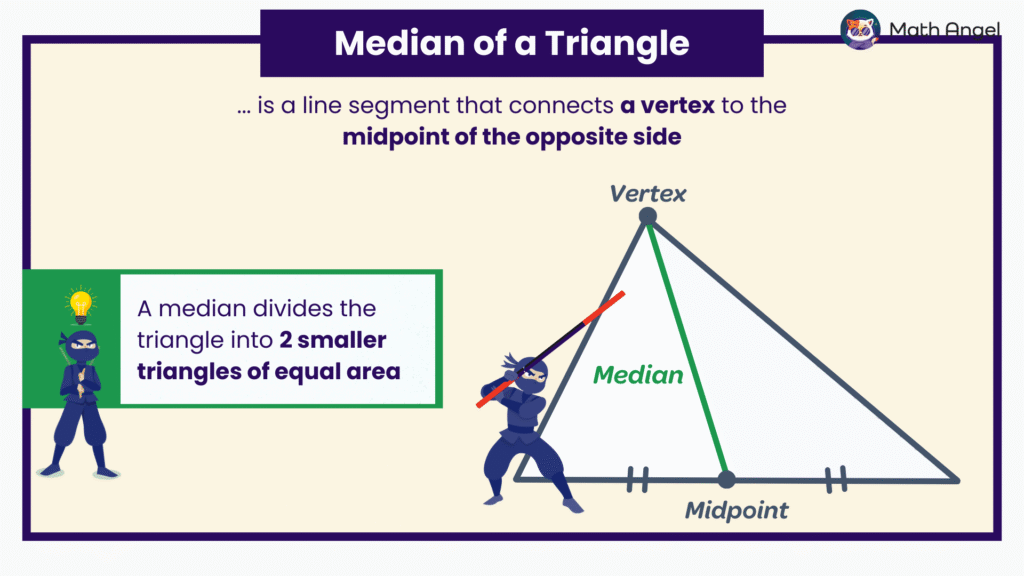
🛎 Definition of a Median:
A median of a triangle is a line segment that connects a vertex to the midpoint of the opposite side.
🛎 A Key Property of a Median:
A median divides the triangle into two smaller triangles of equal area, no matter what the triangle looks like.
What is Centroid of a Triangle?
⏩️
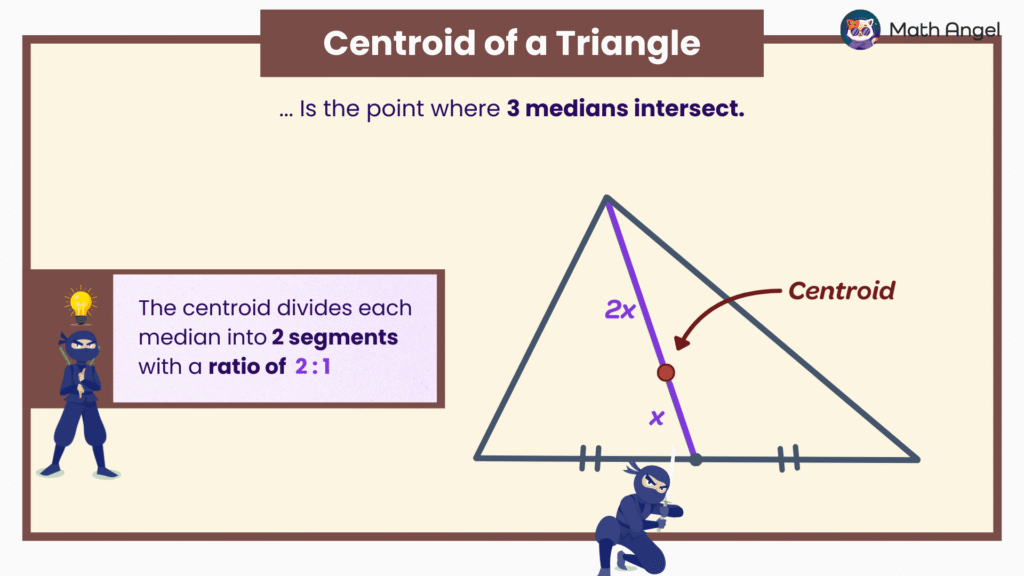
🛎 Definition of a Centroid:
The centroid of a triangle is the point where all three medians intersect.
🛎 A Key Property of a Centroid:
The centroid has a special property: It divides each median into two segments in a ratio of 2:1.
That means the part of the median from the vertex to the centroid is twice as long as the part from the centroid to the midpoint of the side
Practice: Median and Centroid of a Triangle
⏩️
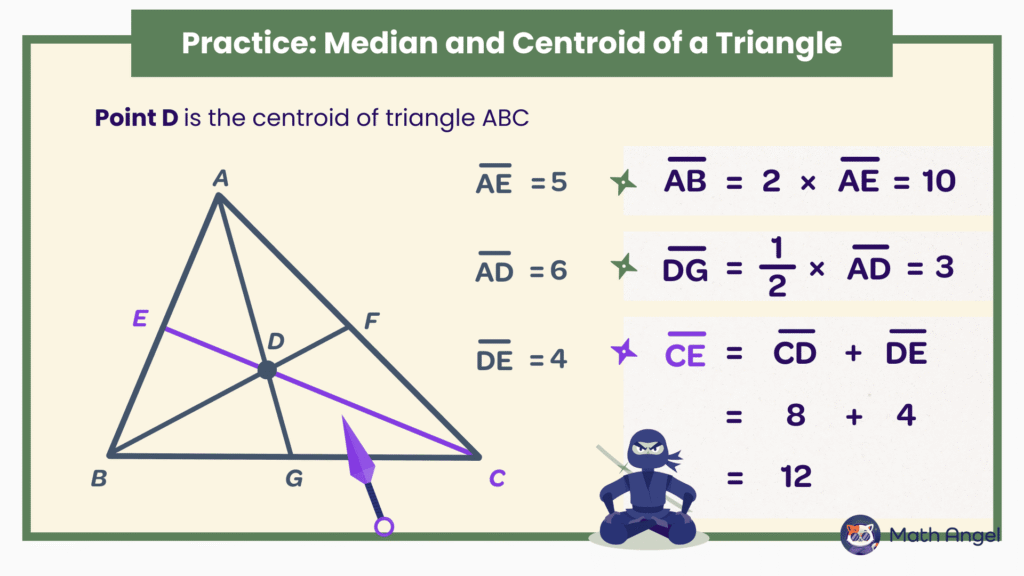
Point D is the centroid of triangle ABC. Points E, F, G are the midpoints of the sides.
We are given:
- $AE = 5$
- $AD = 6$
- $DE = 4$
Now let’s find some missing lengths:
1. Find $AB$
Since $E$ is the midpoint of $AB$,
$AB = 2 \times AE = 2 \times 5 = 10$
2. Find $DG$
Since $D$ is the centroid, it divides each median in a $2:1$ ratio.
So $DG = \tfrac{1}{2} \times AD = \tfrac{1}{2} \times 6 = 3$
3. Find $CE$
$CE = CD + DE$
Since $D$ is the centroid, $CD = 2 \times DE = 2 \times 4 = 8$
So $CE = 8 + 4 = 12$
🍪 Quiz: Practice Medians and Centroid of Triangles
🎩 Stuck on Geometry Problems? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

