Numbers and Decimals

Basic Arithmetic

Number Line and Comparing Numbers

Place Value and Rounding Numbers

Basic Arithmetic and Inverse Operations

BIDMAS - Order of Operations

Commutative Property and Associative Property

Distributive Property

Column Addition and Column Subtraction

Long Multiplication

Factors and Multiples

Divisibility and Divisibility Rules

Prime Numbers and Prime Factorization

How to Find HCF and LCM

Powers and Roots

Powers and Indices

Basics of Square Roots

Multiplying and Dividing Square Roots

The nth Root and Fractional Indices

Laws of Indices (Same Base, Same Indices)

Negative Exponents and Power of a Power

Decimals

Decimals and Fractions

Comparing and Rounding Decimals

1 of 2

Previous Lesson

{results_count} Math videos for {phrase}

Displaying {results_count} results of {results_count_total}

Generic filters

Exact matches only

Search in title

Search in content

Search in excerpt

Filter by Lesson Categories

Long Division

Numbers and Decimals Long Division

Courses Overview

🎬 Video Tutorial

(0:20) Setting Up Long Division: Place the divisor on the left and the dividend on the right. Check how many times the divisor fits into the initial digits of the dividend to start the process.
Bringing Down Digits: After each subtraction, bring down the next digit in the dividend. This step-by-step approach is key to calculating the quotient accurately.
(1:15) Understanding Remainders: If there are no more digits to bring down, the remaining number becomes the remainder.
(1:30) Verifying Results: Always check by reversing the division: Quotient × Divisor + Remainder = Dividend. This step confirms the accuracy of your long division result.

📂 Revision Cards

Long division example solving 364 divided by 30, showing steps with quotient 12 and remainder 4, including a check with reverse calculation. — 1) Long Division Example 1

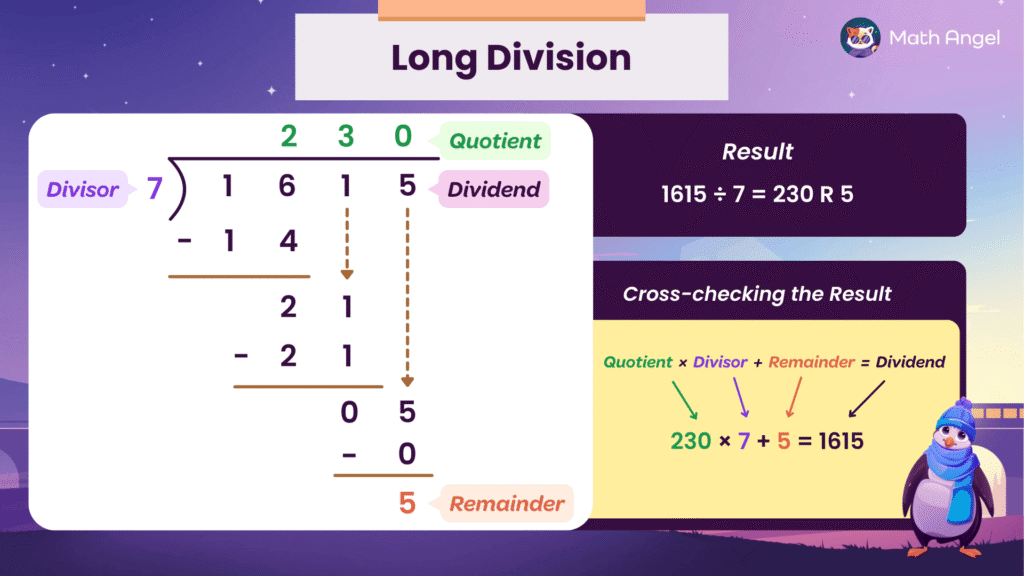
Long division example of 1615 divided by 7, showing step-by-step process with a final result of 230 remainder 5. — 2) Long Division Example 2

🍪 Quiz Time - Practice Now!

0%

Long Division

1 / 6

Q: $75 \div 9 = ?$

7 R5

8 R4

7 R4

8 R3

Feedback: Not quite! To divide 75 by 9, calculate how many times 9 fits into 75. Since 9 × 8 = 72, it fits 8 times with a remainder of 75 - 72 = 3.

Feedback: Well done! To divide 75 by 9, calculate how many times 9 fits into 75. Since 9 × 8 = 72, it fits 8 times with a remainder of 75 - 72 = 3.

2 / 6

Q: $53 \div 6 = ?$

8 R6

7 R5

8 R5

9 R1

Feedback: Not quite! To divide 53 by 6, calculate how many times 6 fits into 53. Since 6 × 8 = 48, it fits 8 times with a remainder of 53 - 48 = 5.

Feedback: Well done! To divide 53 by 6, calculate how many times 6 fits into 53. Since 6 × 8 = 48, it fits 8 times with a remainder of 53 - 48 = 5.

3 / 6

Q: $126 \div 11 = ?$

11 R5

11 R4

12 R5

12 R4

Feedback: Not quite! To divide 126 by 11, calculate how many times 11 fits into 126. Since 11 × 11 = 121, it fits 11 times with a remainder of 126 - 121 = 5.

Feedback: Well done! To divide 126 by 11, calculate how many times 11 fits into 126. Since 11 × 11 = 121, it fits 11 times with a remainder of 126 - 121 = 5.

4 / 6

Q: $325 \div 15 = ?$

21 R10

21 R7

22 R8

22 R5

Feedback: Not quite! To divide 325 by 15, calculate how many times 15 fits into 325. Since 15 × 21 = 315, it fits 21 times with a remainder of 325 - 315 = 10.

Feedback: Well done! To divide 325 by 15, calculate how many times 15 fits into 325. Since 15 × 21 = 315, it fits 21 times with a remainder of 325 - 315 = 10.

5 / 6

Q: $289 \div 14 = ?$

20 R5

20 R9

19 R7

19 R3

Feedback: Not quite! To divide 289 by 14, check how many times 14 fits into 289. Since 14 × 20 = 280, it fits 20 times with a remainder of 289 - 280 = 9.

Feedback: Well done! To divide 289 by 14, check how many times 14 fits into 289. Since 14 × 20 = 280, it fits 20 times with a remainder of 289 - 280 = 9.

6 / 6

Q: $1053 \div 47 = ?$

22 R29

23 R25

22 R19

23 R19

Feedback: Not quite! Dividing 1053 by 47, calculate how many times 47 fits into 1053. Since 47 × 22 = 1034, there is a remainder of 1053 - 1034 = 19.

Feedback: Well done! Dividing 1053 by 47, calculate how many times 47 fits into 1053. Since 47 × 22 = 1034, there is a remainder of 1053 - 1034 = 19.

Your score is

The average score is 30%

0%

🎩 AI Math Solver (ChatCat)

Need math help? Chat with our AI Math Solver at the bottom right!

Previous Lesson

4 2 votes

Article Rating

Label

Name*

Email

Label

Name*

Email

0 Comments

Newest

Oldest Most Voted

Inline Feedbacks

View all comments

Post a comment

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Comment *

Name

Email

Website

Save my name, email, and website in this browser for the next time I comment.

Log In

Username or Email Address

Password

Remember Me

Join Now | Lost Password?

Login

Accessing this course requires a login. Please enter your credentials below!

Username or Email Address

Password

Remember Me

Lost Your Password?

Register

Don't have an account? Register one!

Register an Account