How to Combine Ratios
Table Of Contents
🎬 Math Angel Video: How to Combine Ratios
How to Combine Ratios?
⏩️
Sometimes, we are given two ratios that share one common term.
To combine them into a single ratio, we need to make sure the shared term is the same in both ratios.
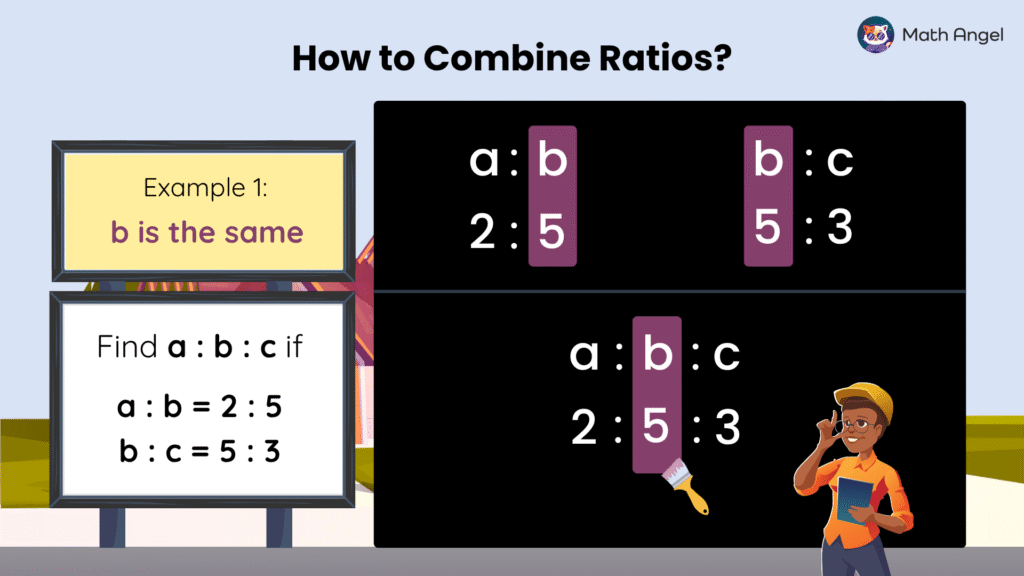
🛎️ Example: Combining Two Ratios into One
$$a : b = 2 : 5$$
$$b : c = 5 : 3$$
Here, the common term is $b$. Notice that both ratios already have $b = 5$, so we can directly combine them by writing them together.
So the final answer is:
$$a : b : c = 2 : 5 : 3$$
❇️ Tip: Always check that the middle terms (the shared ones) match before combining. If they don’t, you’ll need to scale one or both ratios until they do.
How to Combine Two Ratios Using LCM
⏩️
Sometimes the shared term is different in each ratio. In this case, we need to make the shared term the same by using the Lowest Common Multiple (LCM).
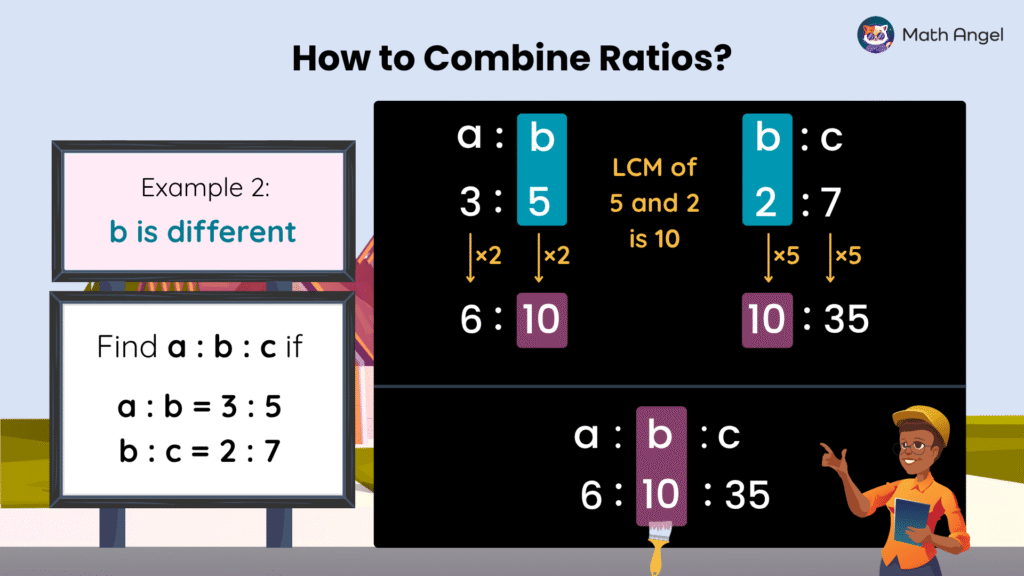
🛎️ Example: Combining Two Ratios into One Using LCM
$$a : b = 3 : 5$$
$$b : c = 2 : 7$$
Here, the common term is $b$, but in the first ratio $b = 5$ and in the second ratio $b = 2$. We need to scale both ratios so that b becomes the same.
- Step 1: Find the LCM
The LCM of $5$ and $2$ is $10$. - Step 2: Scale the ratios
- Multiply $a : b = 3 : 5$ by $2$ to get $a : b = 6 : 10$
- Multiply $b : c = 2 : 7$ by $5$ to get $b : c = 10 : 35$
- Step 3: Combine into one ratio
Now that $b = 10$ in both, the final answer is:
$$a : b : c = 6 : 10 : 35$$
Combining Ratios Step by Step (Real-Life Example)
⏩️
⏩️
In exam questions, ratios often appear in real-life contexts, like mixing materials or ingredients.
We still use the same method: make the shared term equal, then combine.
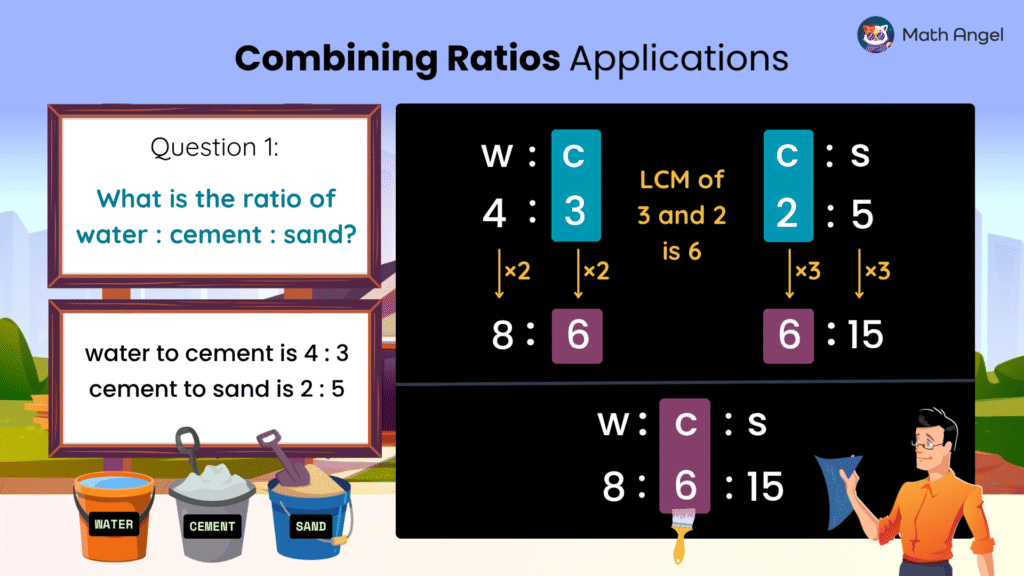
🛎️ Application: Combining Ratios
Water to cement is given as $4 : 3$.
Cement to sand is given as $2 : 5$.
Q1: Find the ratio of water : cement : sand.
Q2: If you have 24 buckets of water, how many buckets of sand do you need?
- Step 1: Identify the common term
The common term is cement. - Step 2: Find the LCM
In the first ratio, cement $= 3$, and in the second ratio, cement $= 2$.
The LCM of $3$ and $2$ is $6$. - Step 3: Scale the ratios
- Multiply $4 : 3$ by 2 to get $ 8 : 6$
- Multiply $2 : 5$ by 3 to get $ 6 : 15$
- Step 4: Combine into one ratio
Now that cement is the same in both, the combined ratio is:
$$Water : Cement : Sand = 8 : 6 : 15$$
- Step 5: Scale up so that water = 24
Since $8 \times 3 = 24$, multiply the whole ratio by 3:
$$Water : Cement : Sand = 24 : 18 : 45$$
- Final Answer:
If you have 24 buckets of water, you need 45 buckets of sand.
🍪 Quiz: Practicing Combining Two Ratios Into One
🎩 Stuck on Ratio Problems? Ask Your AI Buddy
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
