Directly Proportional and Inversely Proportional
Table Of Contents
🎬 Math Angel Video: Direct Proportion vs Inverse Proportion
What Does “Directly Proportional” Mean?
⏩️
🛎️ Directly Proportionality Definition:
When two quantities are directly proportional, as one increases or decreases, the other increases or decreases by the same factor.
🛎️ Key Features of Direct Proportionality:
- If you double one quantity, the other will also double.
- If you triple one quantity, the other will triple too.
- If you halve one quantity, the other will also halve.
🛎️ Example of Direct Proportionality:
Imagine you are buying watermelons at a shop. Each watermelon costs £4.
The total cost is directly proportional to the number of watermelons you buy, because each one costs the same amount.
| Number of Watermelons | Total Cost |
|---|---|
| 1 | £4 = 1 x £4 |
| 3 | £12 = 3 x £4 |
| 5 | £20 = 5 x £4 |
| 8 | £32 = 8 x £4 |
| 10 | £40 = 10 x £4 |
You can calculate the total cost using this formula:
$$\text{Total Cost} = \text{Number of Watermelons} \times £4$$
What Is Inversely Proportional?
⏩️
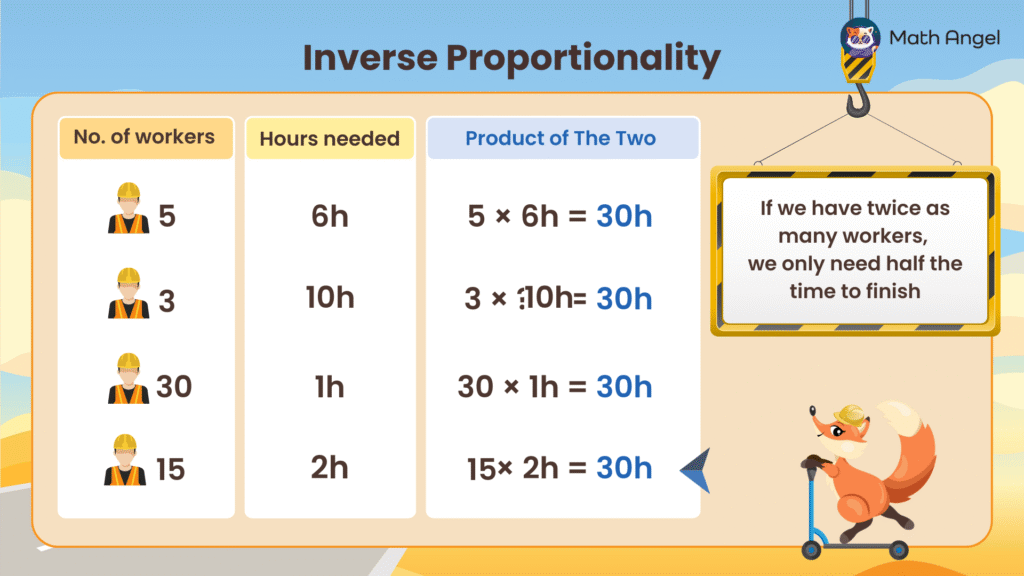
🛎️ Inverse Proportionality Definition:
When two quantities are inversely proportional, it means that as one increases, the other decreases in such a way that their product always stays the same.
🛎️ Key Features of Inverse Proportionality:
- If you double one quantity, the other is halved.
- If you triple one, the other becomes one third as much.
- The product (when you multiply the two quantities together) is always the same.
🛎️ Example of Inverse Proportionality:
Imagine you are working on a job.
- If 5 people work together, it takes 6 hours to finish.
- If only 3 people work, it takes 10 hours to finish.
- If 30 people work, it only takes 1 hour to finish.
| Number of Workers | Hours Needed | Product (Workers × Hours) |
|---|---|---|
| 5 | 6 | 30 |
| 3 | 10 | 30 |
| 30 | 1 | 30 |
| 15 | 2 | 30 |
Notice that if you multiply the number of workers by the number of hours, you always get the same result: 30.
Therefore, the number of workers and the number of hours needed to finish this task is inversely proportional.
You can calculate the number of workers or hours needed using this formula:
$$ \text{Number of Workers} \times \text{Hours Needed} = \text{Constant}$$
❇️ Exam Tip: If the product of the two quantities always stays the same, they are inversely proportional.
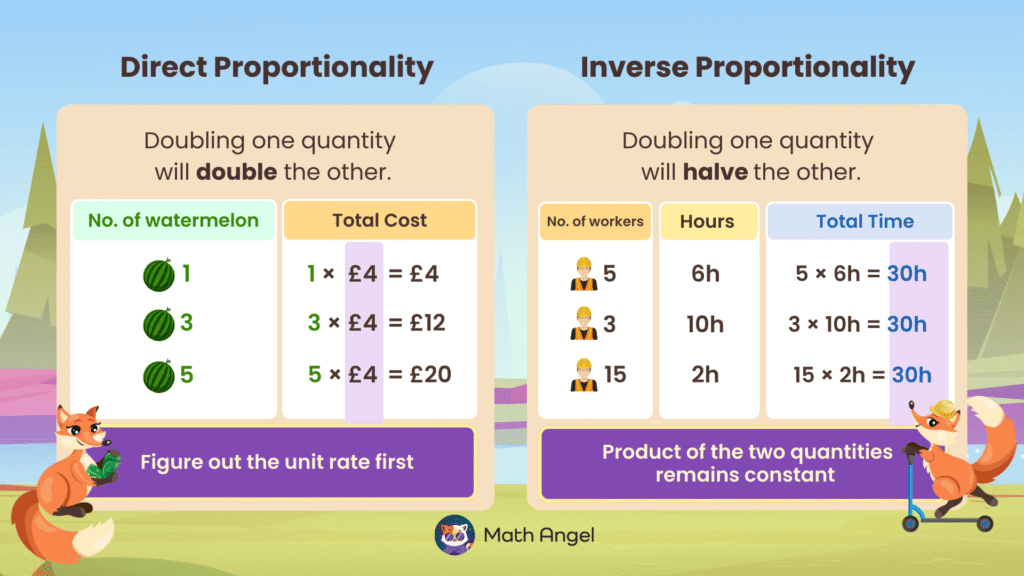
Direct vs Inverse Proportion
⏩️
It’s important to learn how to spot whether a relationship is directly or inversely proportional. This skill often comes up in math exams.
🛎️ How to Spot Direct Proportion:
If you divide one quantity by the other, you always get the same answer.
Example: Divide total cost by number of watermelons → always £4.
This means the total cost is directly proportional to the number of watermelons.
🛎️ How to Spot Inverse Proportion:
If you multiply one quantity by the other, you always get the same answer.
Example: Multiply number of workers by hours needed → always 30.
This means the time needed is inversely proportional to the number of workers.
🍪 Quiz: Direct and Inverse Proportion Practice
🎩 Stuck on Proportionality Problems? Ask Our AI Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
