Convert Fraction to Decimal Using Long Division

Table Of Contents

🎬 Math Angel Video: How Convert Fraction to Decimal Step by Step

Recap: Converting Simple Fractions to Decimals

Converting fractions like 2/5 and 3/4 to decimals using equivalent fractions and prompting 21/16 as a challenge.

⏩️ (0:01)

We can change some fractions into decimals easily by making the denominator 10, 100, or another power of 10.

 

🛎️ Example:

  • $\frac{2}{5} = \frac{4}{10} = 0.4$

  • $\frac{3}{4} = \frac{75}{100} = 0.75$

But not every fraction works this way. For example, the denominator of $\frac{21}{16}$ can’t easily be turned into 10, 100, or 1000.

To convert fractions like this, we’ll need to use long division. That’s what we’ll learn in the next section:)

Fractions to Decimals Using Long Division (Terminating Decimal Example)

Convert fractions to decimals with step-by-step examples 21 ÷ 16 = 1.3125.

⏩️ (1:18)

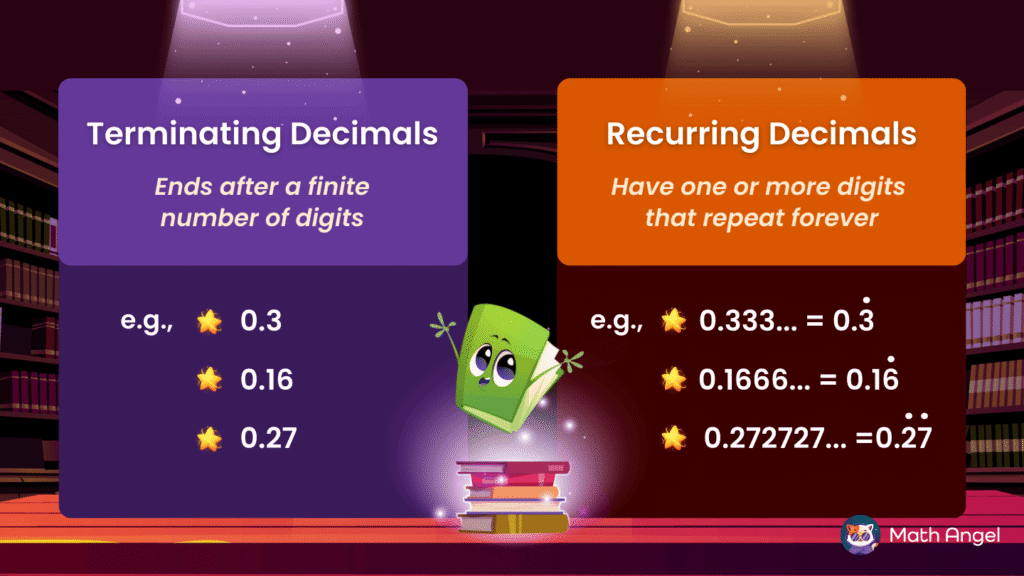
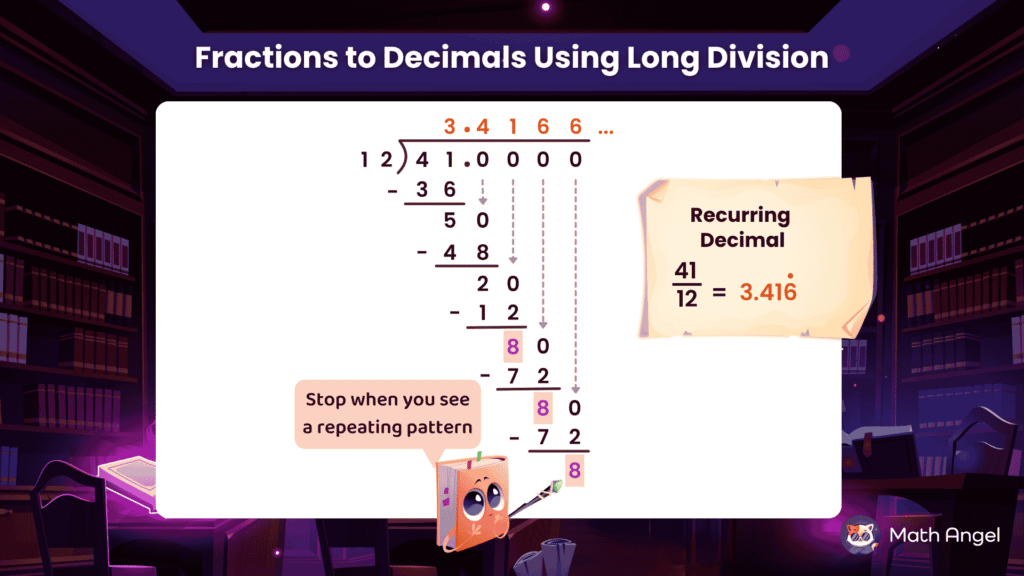
When the denominator doesn’t turn easily into 10 or 100, use long division to change the fraction into a decimal.

 

🛎️ Example: Turn $\frac{21}{16}$ to decimal

We divide 21 ÷ 16 using long division.

  1. 16 goes into 21 once → write1 on top.
    Subtract 16 from 21, the remainder is 5.

  2. Add a decimal point and bring down a 0 to make 50.
    50 ÷ 16 = 3 remainder 2 → write 3 after the decimal.

  3. Bring down another 0.
    20 ÷ 16 = 1 remainder 4 → write 1 on top.

  4. Bring down another 0.
    40 ÷ 16 = 2 remainder 8 → write 2 on top.

  5. Bring down another 0.
    80 ÷ 16 = 5 remainder 0 → write 5 on top.

❇️ When the remainder becomes 0, you can stop.

$$\frac{21}{16} = 1.3125$$

1.3125 is a terminating decimal because it has a finite number of digits.

Terminating Decimals vs. Recurring Decimals

Comparison of terminating and recurring decimals with examples 0.3 and 0.33333…

⏩️ (1:47)

When we convert fractions to decimals, they can be either terminating or recurring.

 

🛎️ Terminating Decimals

Terminating decimals end after a certain number of digits.

$$
0.3, \quad 0.16, \quad 0.27
$$

 

🛎️ Recurring Decimals

These have one or more digits that repeat forever.
We show the repeating part with a dot $(\cdot)$ or a bar $(\overline{\phantom{0}})$ above the repeating digits.

$$
0.333\ldots = 0.\overline{3}
$$

$$
0.1666\ldots = 0.1\overline{6}
$$

$$
0.272727\ldots = 0.\overline{27}
$$

Fractions to Decimals Using Long Division (Recurring Decimal Example)

Conversion of fractions to decimals using long division, and recurring decimals (41/12 = 3.416…).

⏩️ (2:32)

When the denominator doesn’t turn easily into 10 or 100, use long division to change the fraction into a decimal.

 

🛎️ Example: Convert $\frac{41}{12}$ to decimal

We divide 41 ÷ 12 using long division.

  1. 12 goes into 41 three times → write 3 on top.
    Subtract 36 from 41, the remainder is 5.

  2. Add a decimal point and bring down a 0 to make 50.
    50 ÷ 12 = 4 remainder 2 → write 2 after the decimal.

  3. Bring down another 0.
    20 ÷ 12 = 1 remainder 8 → write 8 on top.

  4. Bring down a 0.
    80 ÷ 12 = 6 remainder 8 (again!)→ write 8 on top.

❇️ You can stop now, because you see the remainder start repeating.

$$\frac{41}{12} = 3.4166\ldots = 3.41\overline{6}$$

3.4166…. is called a recurring decimal because one or more digits repeat endlessly.

🍪 Practice: Converting Fractions to Decimals

0%

Fractions to Decimals Using Long Division

1 / 6

Q: Convert 11/20 to a decimal.

2 / 6

Q: What is 13/50 as a decimal?

3 / 6

Q: What is 7/8 as a decimal?

4 / 6

Q: Convert 131/99 to a decimal.

5 / 6

Q: What is the decimal equivalent of 7/9?

6 / 6

Q: Convert 87/16 to a decimal.

Your score is

The average score is 50%

0%

🎩 Stuck on Decimals or Fractions? Try AI Math Solver

Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

Previous Lesson
Back to Course
Next Lesson
2 Comments
5 1 vote
Article Rating
guest
2 Comments
Newest
Oldest Most Voted
Inline Feedbacks
View all comments

Leave a Comment

Your email address will not be published. Required fields are marked *