Cavalieri’s Principle
Table Of Contents
🎬 Math Angel Video: Cavalieri’s Principle Explained
An Example of Cavalieri’s Principle
⏩️
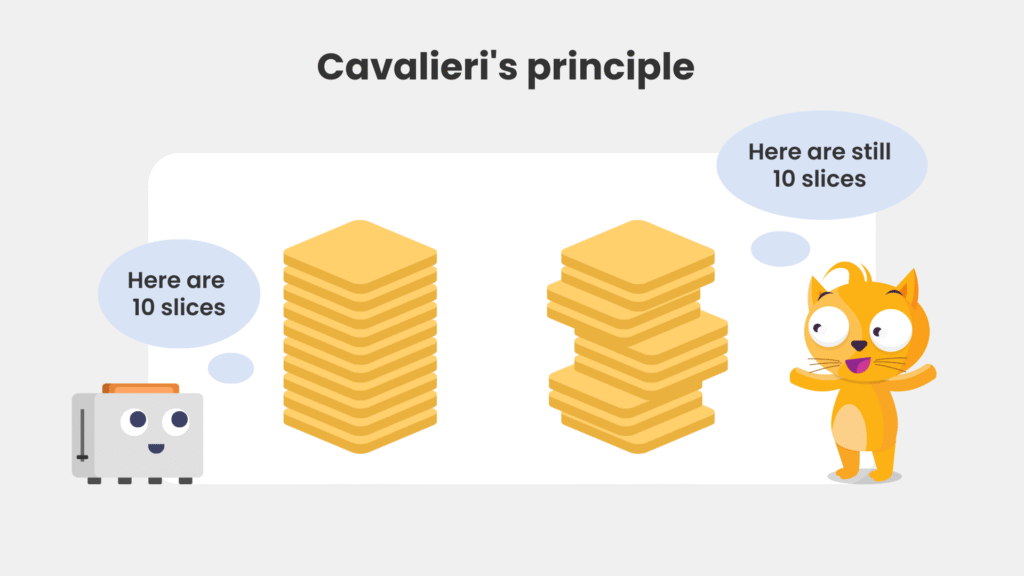
🛎️ Imagine you have 10 slices of bread.
- On the left, the slices are stacked neatly.
- On the right, they are slanted.
Even though the shapes look different, the number and size of the slices are the same, so the total volume is unchanged.
This is a simple example to show how volume can stay the same, even if the shape looks different.
What is Cavalieri’s Principle?
⏩️
Cavalieri’s principle states that if two solids have the same height and same cross-sectional areas, they have the same volume, even if they look different.
In other words, two solids have the same volume if:
- They have the same height, and
- At every level, their cross-sectional areas are the same.
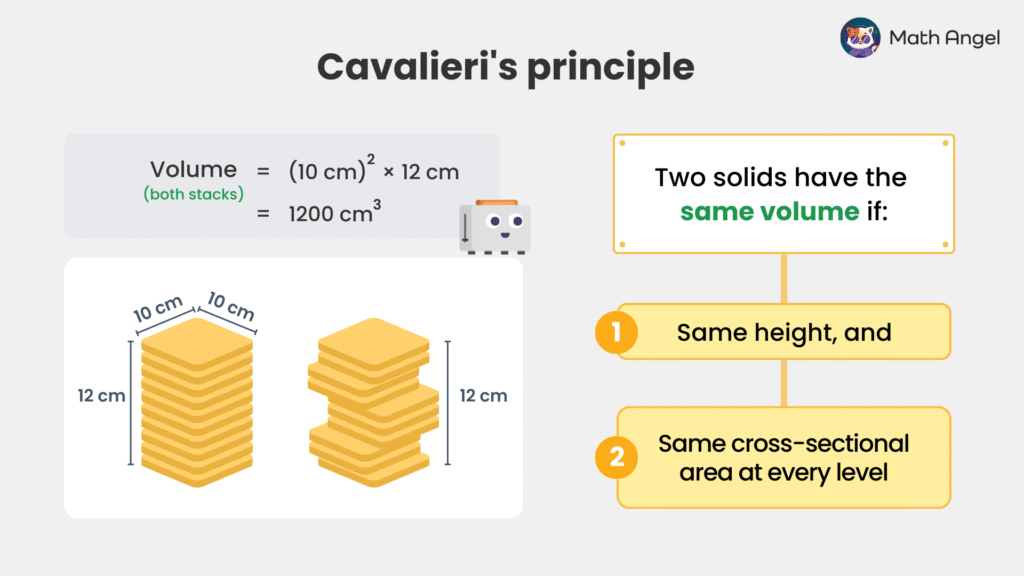
Cavalieri’s Principle can be very helpful. For example, both stacks have a 10 cm by 10 cm base and are 12 cm high.
The neat stack on the left has a volume of:
$$ \text{Volume} = (10 \text{ cm})^2 \times 12\text{ cm} = 1200 \text{ cm}^3$$
Here’s the clever part: by Cavalieri’s Principle, the slanted stack on the right must also have the same volume.
This principle gives us a shortcut: instead of working out the volume of a complicated or tilted solid directly, we can compare it to a simpler ones.
Using Cavalieri’s Principle in 3D
⏩️
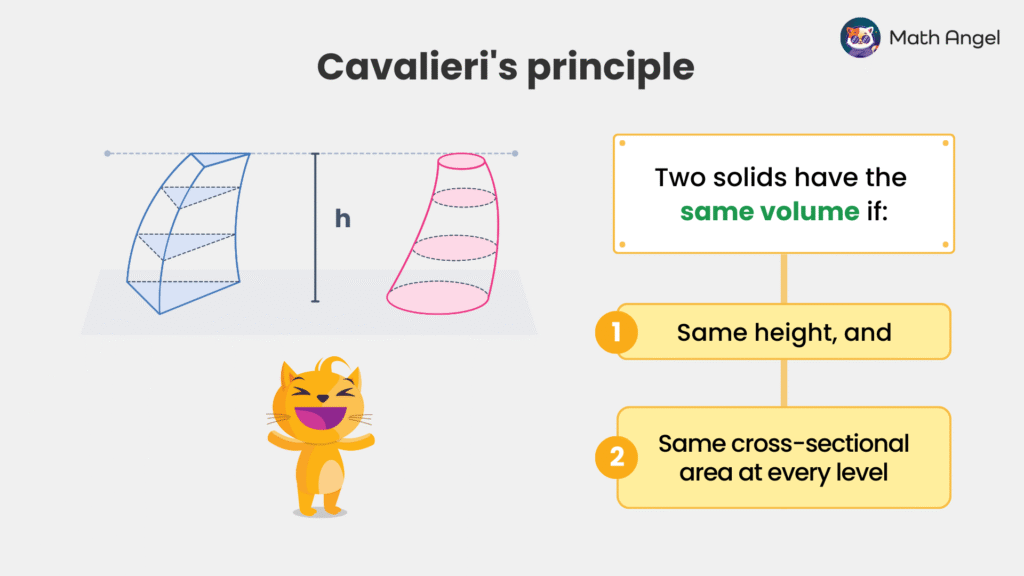
Cavalieri’s Principle doesn’t just work with stacks of slices, it also works for any 3D solids.
If two solids have the same height and the same cross-sectional area at every level, then their volumes are equal, even if the solids look very different.
In the picture, the two shapes both have the same height. At each level, their cross-sections match in area.
So, even though one looks curved and the other looks slanted, they must have the same volume.
This is why Cavalieri’s Principle is such a powerful tool in geometry: it helps us compare and calculate volumes of unusual 3D shapes.
🍪 Quiz: Practice Cavalieri’s Principle in 3D Shapes
🎩 Stuck on Geometry Problems? Ask AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
