Area of a Triangle
Table Of Contents
🎬 Math Angel Video: How to Find the Area of a Triangle
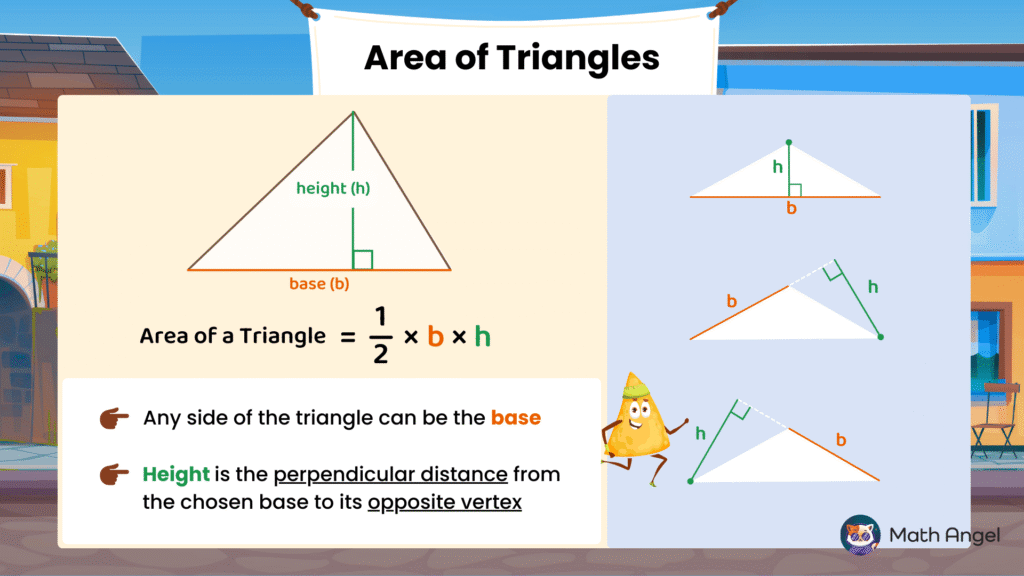
What’s the Formula for the Area of a Triangle?
⏩️
🛎️ The formula to calculate the area of any triangle is:
$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$$
Base ($b$): You can choose any side of the triangle to be the base.
Height ($h$): This is the perpendicular distance from the chosen base to the opposite vertex.
❇️ Important Tip for Exam:
- You must use the height that matches the base you chose.
- The height must be perpendicular from the base up to the opposite vertex.
- You can’t just pick any side and any height, they must be a pair.
How to Find the Area of a Triangle?
⏩️
To find the area of any triangle, use this formula:
$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$$
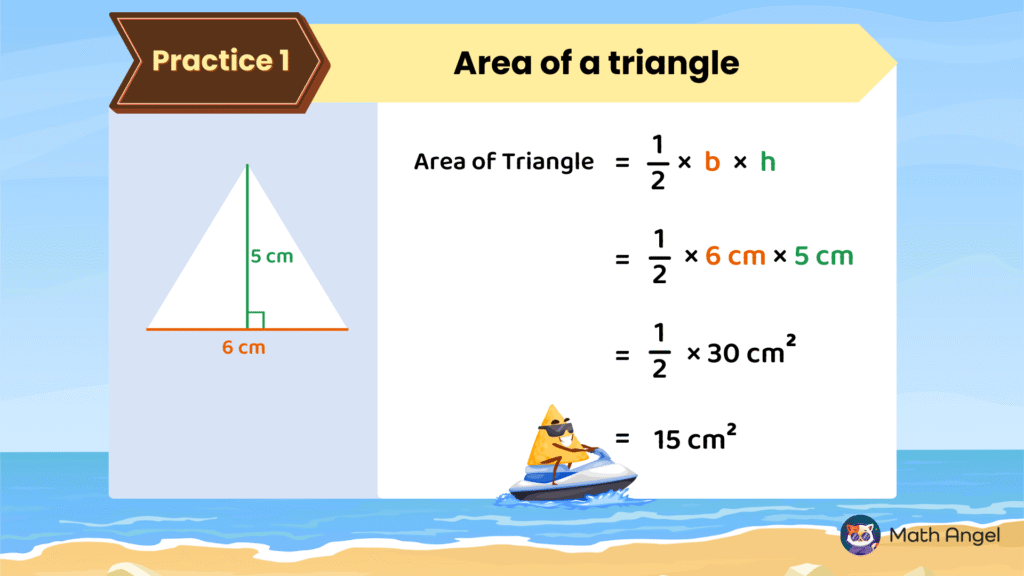
🛎️ Example of Finding the Triangle Area:
Let’s find the area of this triangle:
Base ($b$) = $6\ \text{cm}$
Height ($h$) = $5\ \text{cm}$
Plug the numbers into the formula:
$$
\begin{align}
\text{Area} &= \frac{1}{2} \times 6\ \text{cm} \times 5\ \text{cm} \\[0.5em]
&= \frac{1}{2} \times 30\ \text{cm}^2 \\[0.5em]
&= 15\ \text{cm}^2
\end{align}
$$
So, the area of the triangle is $15\ \text{cm}^2$.
Finding the Area of a Right-Angled Triangle
⏩️
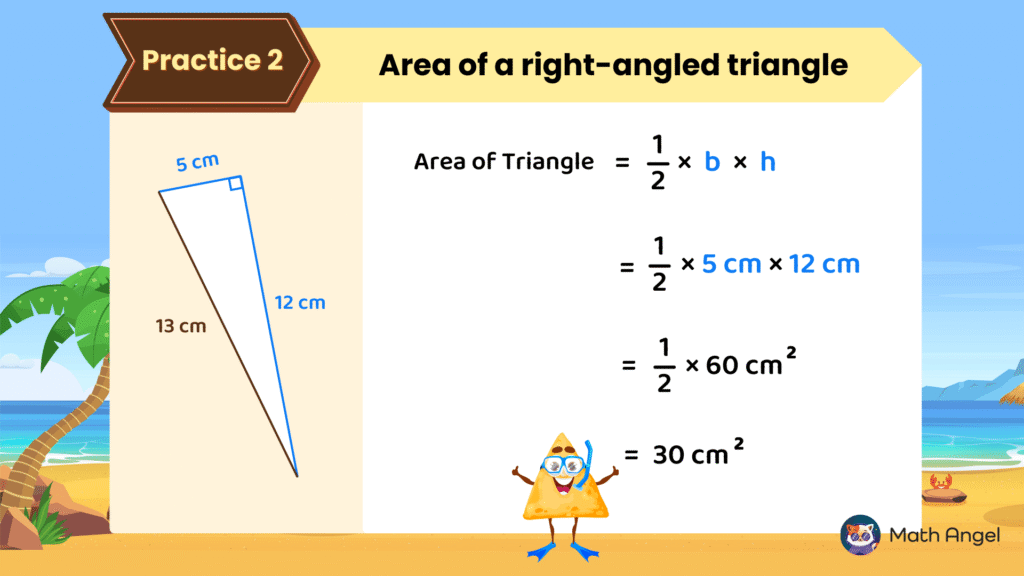
In a right-angled triangle:
The base and height are always the two shorter sides that meet at the right angle. They are called the legs.
The longest side is called the hypotenuse. Do not use the hypotenuse in the area formula.
🛎️ Example: Area of a Right-Angled Triangle
Suppose you have a right-angled triangle with sides of 5 cm, 12 cm, and 13 cm. Find its area.
- Step 1: Identify the base and height:
The two shorter sides (5 cm and 12 cm) are the legs.
The longest side (13 cm) is the hypotenuse.
Step 2: Use the two legs in the area formula:
$$
\begin{align}
\text{Area} &= \frac{1}{2} \times 5\ \text{cm} \times 12\ \text{cm} \\[0.5em]
&= \frac{1}{2} \times 60\ \text{cm}^2 \\[0.5em]
&= 30\ \text{cm}^2
\end{align}
$$
So, the area of this right-angled triangle is $30\ \text{cm}^2$.
Using Area to Find the Height of a Triangle

⏩️
If you know the area and the base of a triangle, you can find the height using the same formula:
$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$$
This time, you need to rearrange the formula to solve for height.
🛎️ Example: Finding the Triangle Height Using Area Formula
If the area of a triangle is $42\ \text{cm}^2$, and the base is $7\ \text{cm}$. Can you find the height $h$ ?
Set up the formula and solve for $h$:
$$
\begin{align}
\frac{1}{2} \times 7\,\text{cm} \times h &= 42\,\text{cm}^2 \\[0.5em]
7\,\text{cm} \times h &= 42\,\text{cm}^2 \times 2 \\[0.5em]
h &= \frac{84\,\text{cm}^2}{7\,\text{cm}} = 12\,\text{cm}
\end{align}
$$
So, the height of this triangle is $12\ \text{cm}$.
🍪 Quiz (6 Questions): Practice Finding Triangle Area
🎩 Stuck on Area Calculation? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

