Angle Relationships in Intersecting and Parallel Lines
Table Of Contents
🎬 Math Angel Video: Angle Relationships Explained
Angle Relationships of Two Intersecting Lines
⏩️
When two lines intersect, they form special types of angle relationships:
🛎️ What Are Vertically Opposite Angles?
- Definition: Vertically opposite angles are the angles formed across from each other when two lines intersect.
- Feature: Vertically opposite angles are always equal.
🛎️ What Are Adjacent Angles?
- Definition: Adjacent angles share a common side and a common vertex.
- Key Fact: The sum of two adjacent angles can be any value.
- Special Case: If adjacent angles lie on a straight line, their sum is $180^\circ$.
🛎️ What Are Supplementary Angles?
- Definition: Any two angles that sum to $180^\circ$ are supplementary.
- Key Difference: Supplementary angles are any two angles that sum to $180^\circ$, whether they are adjacent or not.
Angle Relationships in Parallel Lines and a Transversal
⏩️
A transversal is a straight line that crosses two or more other lines.
When a transversal crosses two parallel lines, it forms special pairs of angles
🛎️ What Are Corresponding Angles?
- Corresponding angles are pairs of angles that lie on the same side of the transversal and in the same position at each intersection.
- Corresponding angles are equal if the lines are parallel.
🛎️ What Are Alternate Interior Angles?
- Alternate interior angles are pairs of angles that lie between the two lines and on opposite sides of the transversal.
- Alternate interior angles are equal if the lines are parallel.
🛎️ What Are Co-Interior Angles?
- Co-interior angles are pairs of angles that lie between the two lines and on the same side of the transversal.
- Co-interior angles add up to $180^\circ$ if the lines are parallel.
Practice: Finding Angles in Parallel Lines
⏩️
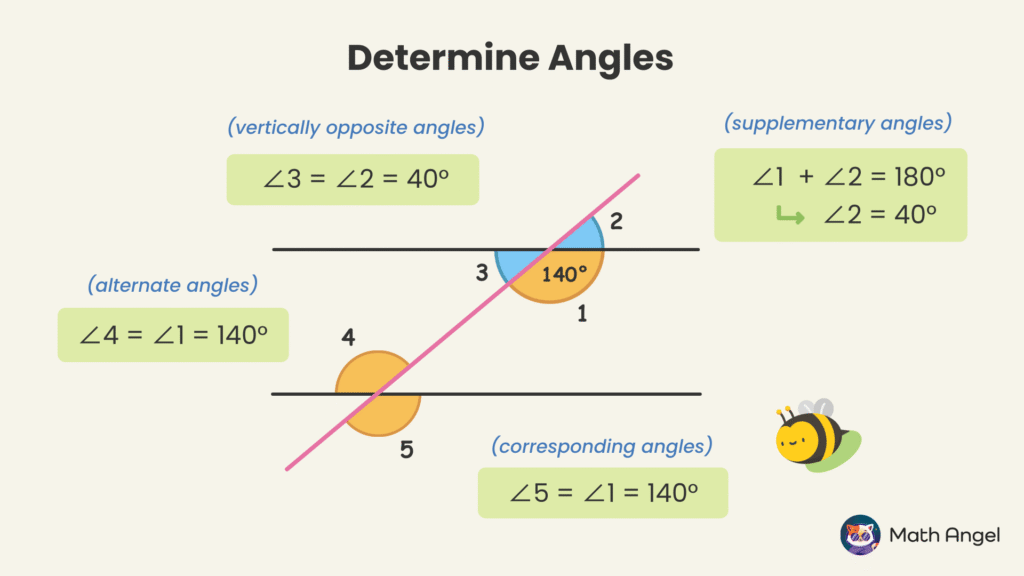
You are given two parallel lines and ∠1 = 140°.
Use the angle rules to find ∠2, ∠3, and ∠4.
∠1 and ∠2 are supplementary angles:
Angles that lie on a straight line add up to 180°.
∠1 + ∠2 = 180° → ∠2 = 40°∠2 and ∠3 are vertically opposite angles:
Vertically opposite angles are equal.
∠3 = ∠2 = 40°∠4 and ∠1 are alternate angles alternate angles:
Alternate angles are equal when lines are parallel.
∠4 = ∠1 = 140°
❇️ Final Answers: ∠2 = 40° ∠3 = 40° ∠4 = 140°
🍪 Quiz: Test Your Skills with Angles in Parallel Lines
🎩 Stuck on Angle Problems? Try Our AI Maths Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
