{results_count} Math videos for {phrase}
Displaying {results_count} results of {results_count_total}
Angle Relationships in Intersecting and Parallel Lines
🎬 Math Angel Video: Angle Relationships Explained
Angle Relationships of Two Intersecting Lines (0:01)
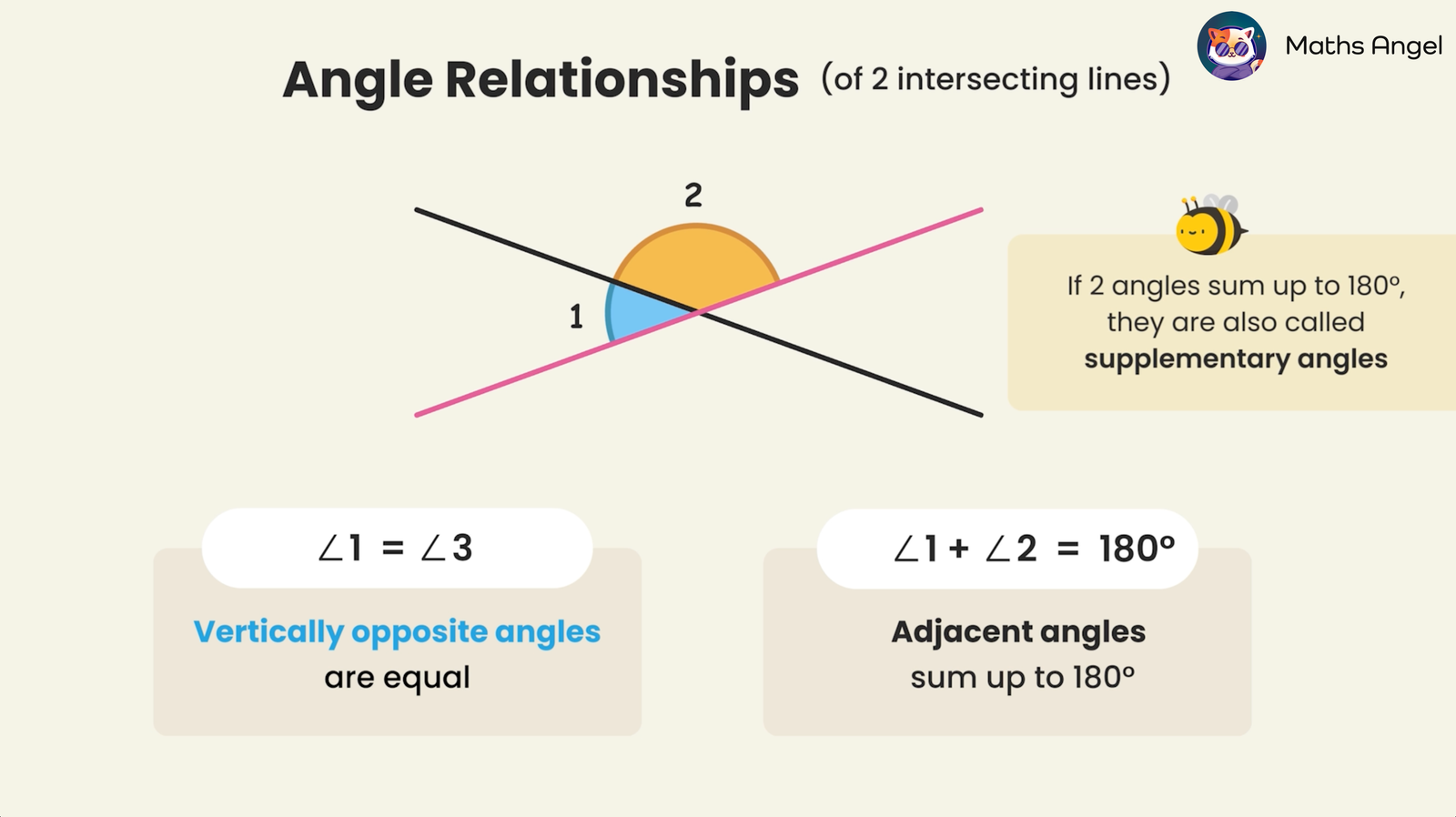
When two lines intersect, they form special types of angle relationships:
🌟 What Are Vertically Opposite Angles?
- Definition: Vertically opposite angles are the angles formed across from each other when two lines intersect.
- Feature: Vertically opposite angles are always equal.
🌟 What Are Adjacent Angles?
- Definition: Adjacent angles share a common side and a common vertex.
- Key Fact: The sum of two adjacent angles can be any value.
- Special Case: If adjacent angles lie on a straight line, their sum is $180^\circ$.
🌟 What Are Supplementary Angles?
- Definition: Any two angles that sum to $180^\circ$ are supplementary.
- Key Difference: Supplementary angles are any two angles that sum to $180^\circ$, whether they are adjacent or not.
Angle Relationships in Parallel Lines and a Transversal (0:45)
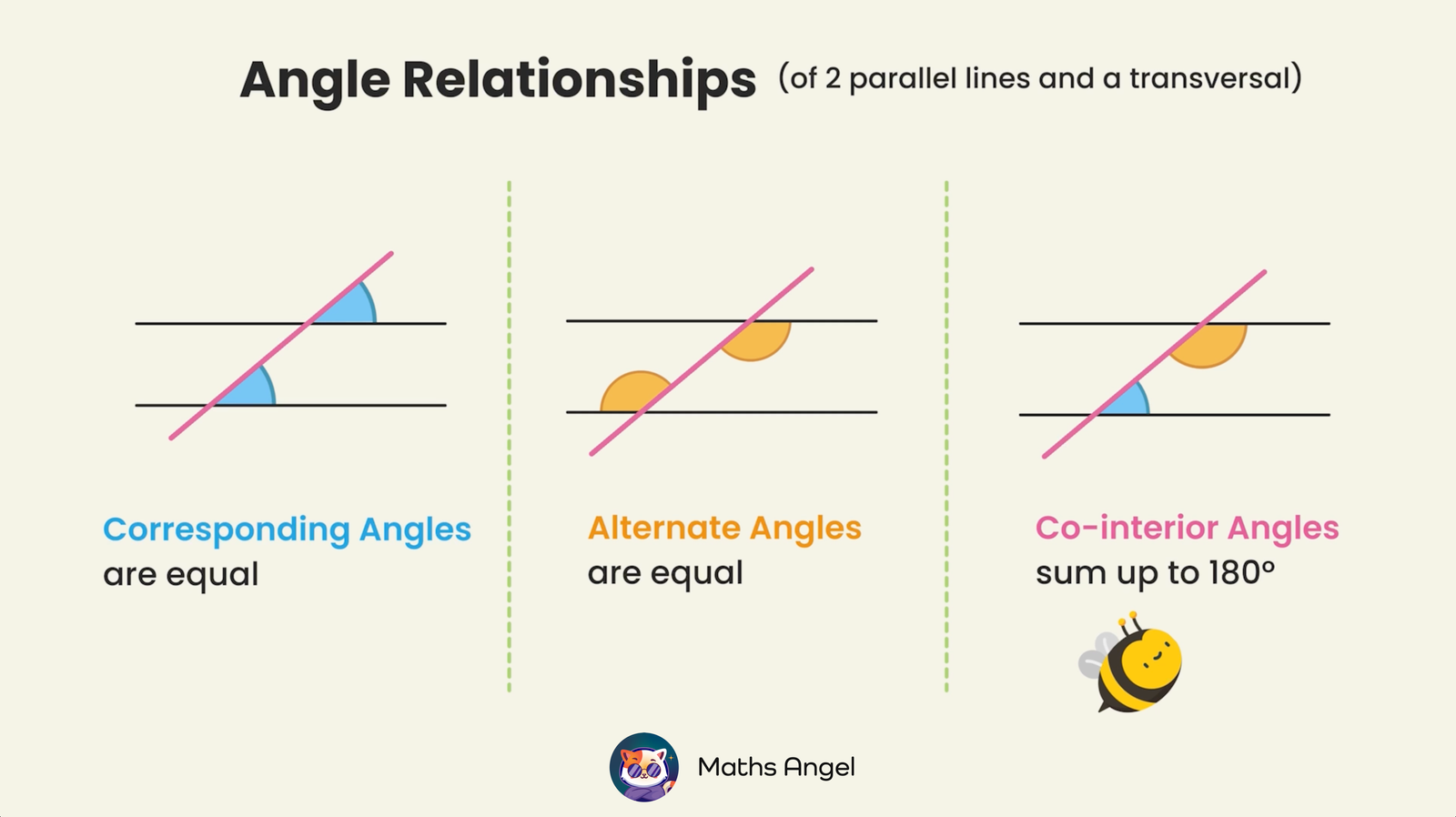
A transversal is a straight line that crosses two or more other lines.
When a transversal crosses two parallel lines, it forms special pairs of angles:
🌟 What Are Corresponding Angles?
- Corresponding angles are pairs of angles that lie on the same side of the transversal and in the same position at each intersection.
- Corresponding angles are equal if the lines are parallel.
🌟 What Are Alternate Interior Angles?
- Alternate interior angles are pairs of angles that lie between the two lines and on opposite sides of the transversal.
- Alternate interior angles are equal if the lines are parallel.
🌟 What Are Co-Interior Angles?
- Co-interior angles are pairs of angles that lie between the two lines and on the same side of the transversal.
- Co-interior angles add up to $180^\circ$ if the lines are parallel.
📂 Flashcards: Corresponding, Alternative, and Co-interior Angles
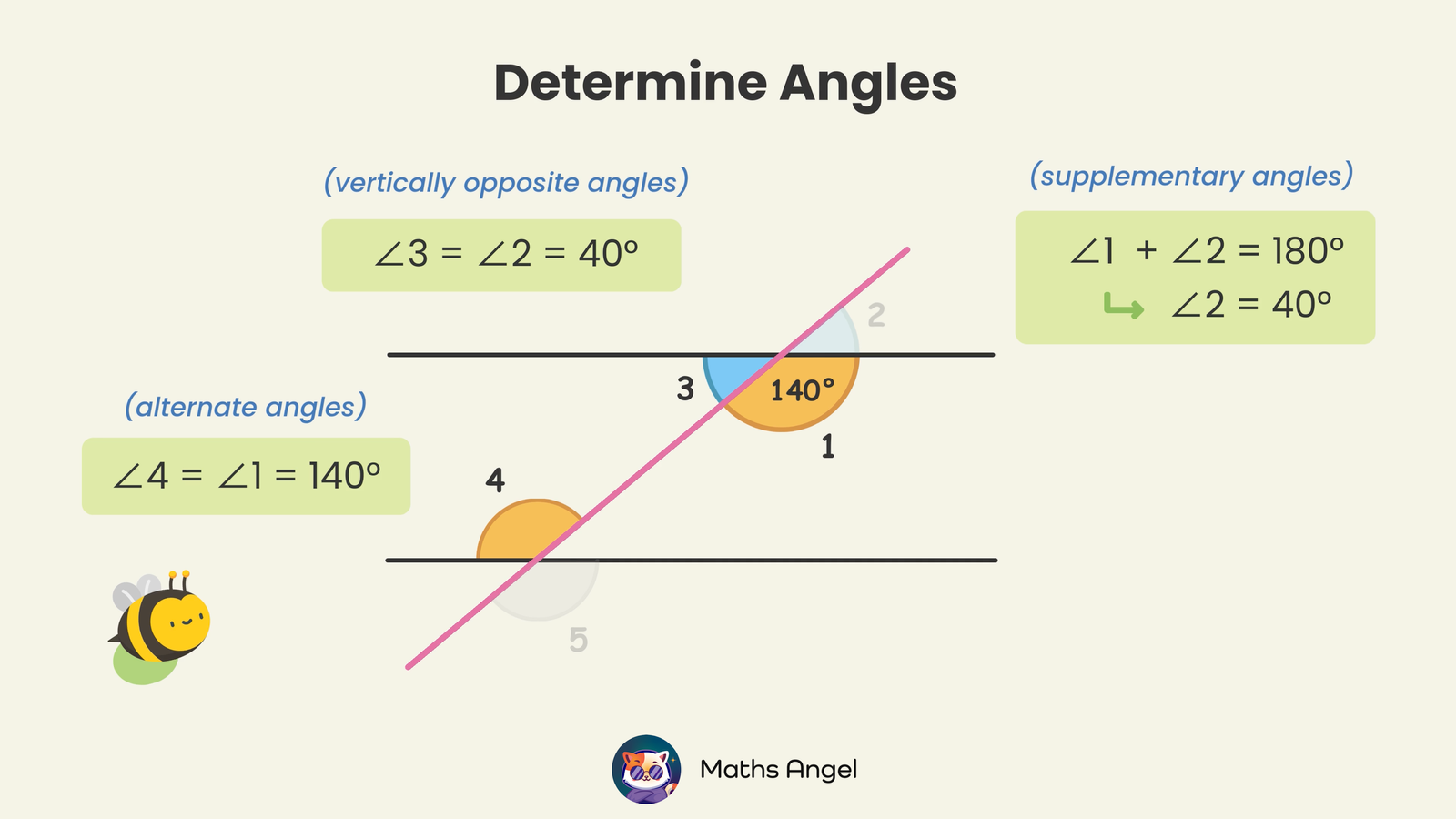
🍪 Quiz: Test Your Skills with Angles in Parallel Lines
Membership Required
You must be a member of Math Angel Plus or Math Angel Unlimited to view this content.
Already a member? Log in here
🎩 Stuck on Angle Problems? Try Our AI Maths Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
5
4
votes
Article Rating
0 Comments
Newest
Oldest
Most Voted
Inline Feedbacks
View all comments

