Volume of a Cuboid and Cube
Table Of Contents
🎬 Math Angel Video: Volume for Cuboids and Cubes
How to Find the Volume of a Cuboid and a Cube?

⏩️
🛎️ Formula to Calculate the Volume of a Cuboid
$$ \text{Volume} = l \times w \times h $$
Where:
- $l$ is the length
- $w$ is the width
- $h$ is the height
Example: What is the volume of a cuboid with:
- Length = $5\,\text{cm}$
- Width = $3\,\text{cm}$
- Height = $2\,\text{cm}$
$$
V = 5\,\text{cm} \times 3\,\text{cm} \times 2\,\text{cm} = 30\,\text{cm}^3
$$
❇️ Answer: So the volume of this cuboid is 30 cubic centimetres.
🛎️ Formula to Calculate the Volume of a Cube
A cube is a special type of cuboid where the length, width, and height are all equal.
$$ \text{Volume} = s \times s \times s $$
Where:
- $s$ is the length of each side
Example: What is the volume of a cube with:
- Side length = $5 \text{cm}$
$$ V = 5\,\text{cm} \times 5\,\text{cm} \times 5\,\text{cm} = 125\,\text{cm}^3$$
❇️ Answer: So the volume of this cube is 125 cubic centimetres.
How to Find Missing Width of a Cuboid?

⏩️
You can rearrange the volume formula to find a missing dimension.
For example:
- Volume = $120 \text{m}^3 $
- Length $ l= 10 \text{m} $
- Height $ h= 2 \text{m} $
- We want to know the Width $w$
Step 1: Plug in the known values
$$
120\,\text{m}^3 = 10\,\text{m} \times w \times 2\,\text{m}
$$
Step 2: Multiply the known values
$$
120\,\text{m}^3 = 20\,\text{m}^2 \times w
$$
Step 3: Solve for the width
$$
w = \frac{120\,\text{m}^3}{20\,\text{m}^2} = 6\,\text{m}
$$
❇️ Answer: So the width of this cuboid is 6 metres.
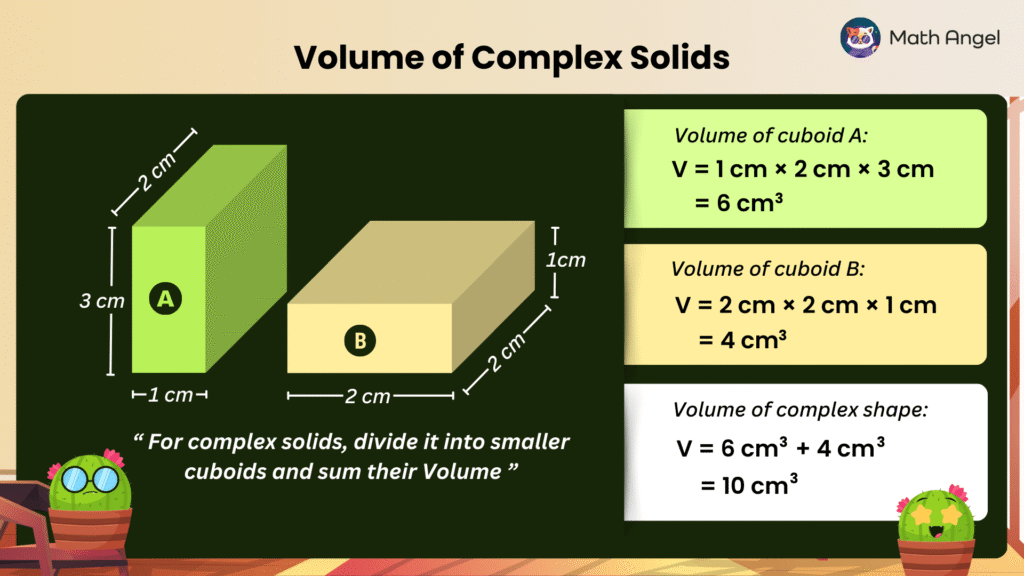
Finding the Volume of a Complex Solid?
⏩️
Method: To find the volume of a complex solid, break it down into smaller cuboids and find the volume of each one. Then add the volumes together.
Example: A complex 3d shape can be split into 2 cuboids.
- For Cuboid A:
$$V = 1\,\text{cm} \times 2\,\text{cm} \times 3\,\text{cm} = 6\,\text{cm}^3$$
- For Cuboid B:
$$V = 2\,\text{cm} \times 2\,\text{cm} \times 1\,\text{cm} = 4\,\text{cm}^3$$
- Adding both together:
$$V = 6\,\text{cm}^3 + 4\,\text{cm}^3 = 10\,\text{cm}^3$$
❇️ Answer: So the volume of the complex solid is 10 cubic centimetres.
Real-Life Application: Volume of a Cuboid

⏩️
Question: If a cuboid-shaped container is being filled with water, and you know the dimensions and the filling speed, you can calculate how long it takes to fill.
- Length = $50\,\text{cm}$
- Width = $30\,\text{cm}$
- Height = $20\,\text{cm}$
Step 1: Calculate the volume of the container
$$ V = 50\,\text{cm} \times 30\,\text{cm} \times 20\,\text{cm} = 30{,}000\,\text{cm}^3$$
Step 2: Convert cubic centimetres to litres
$$ 1{,}000\,\text{cm}^3 = 1\,\text{L} \quad \Rightarrow \quad 30{,}000\,\text{cm}^3 = 30\,\text{L}$$
Step 3: Use the filling speed to find the time
Filling speed = $10,\text{L/min}$
$$ \text{Time} = \frac{30\,\text{L}}{10\,\text{L/min}} = 3\,\text{minutes}$$
❇️ Answer: So, it takes 3 minutes to fill the container.
🍪 Quiz: Practice Finding Volume of Cuboids and Cubes
🎩 Stuck on Cuboid Volume Problems? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

