Surface Area of Solids
Table Of Contents
🎬 Math Angel Video: Surface Area of Cuboids, Cubes, and Prisms
What is the Surface Area of a Solid?
⏩️
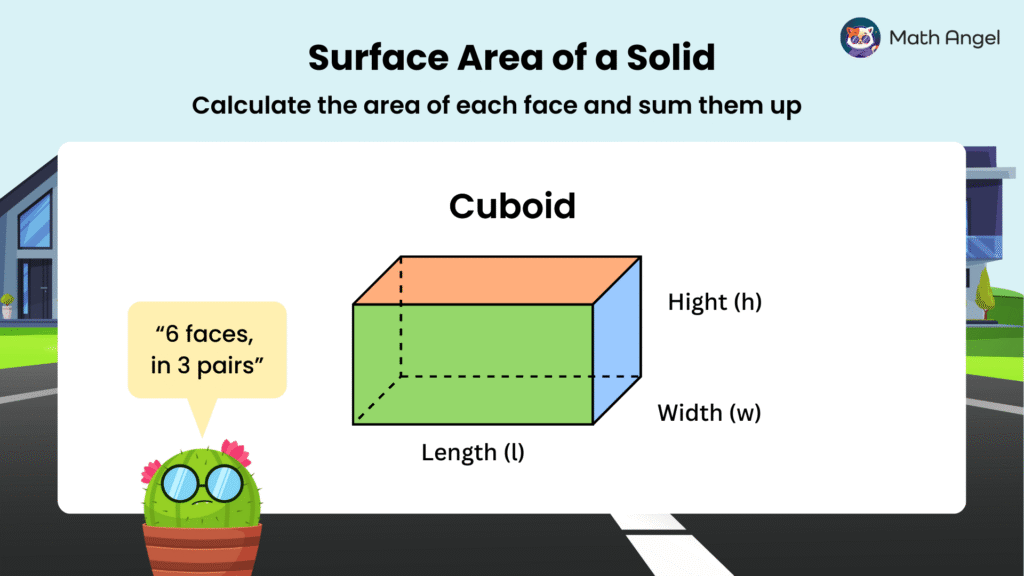
The surface area of a solid is the total area of all its faces (the outside surfaces).
🛎️ Surface Area of a Cuboid:
- A cuboid has 6 faces, grouped in 3 pairs.
- Each pair of faces is the same size.
Let’s call:
- Length = $l$
- Width = $w$
- Height = $h$
To find the total surface area:
- The top and bottom faces are identical. Each has an area of $l \times w$.
- The front and back faces are identical. Each has an area of $l \times h$.
- The left and right faces are identical. Each has an area of $w \times h$.
By adding them all together, you get:
🛎️ Surface Area of a Cuboid Formula:
$$
\large
\begin{align*}
\text{SA} &= 2lw + 2lh + 2wh \\[0.5em]
&= 2(lw + lh + wh)
\end{align*}
$$
❇️ Exam Tip: Remember, every cuboid has 3 different face shapes, and each appears twice:)
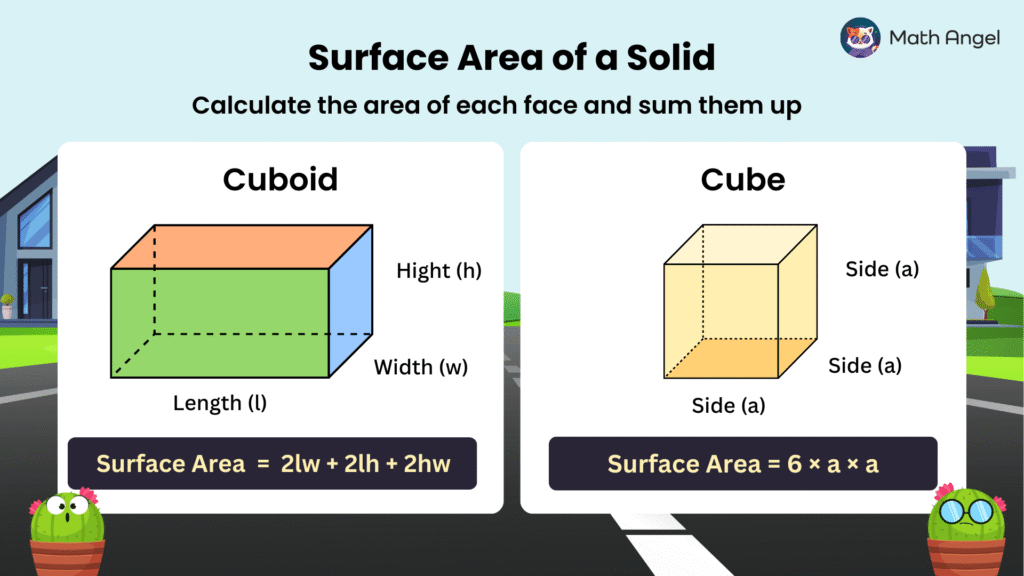
How to Find the Surface Area of a Cube?
⏩️
A cube has 6 identical square faces.
If each side of the cube is $a$:
- Area of each face: $a \times a = a^2$
- Total surface area: 6 faces, so $6 \times a^2$
🛎️ Surface Area of a Cube Formula:
$$ \large \text{SA} = 6a^2$$
❇️ Exam Tip: Every face on a cube is a square, and all 6 faces are same size:)
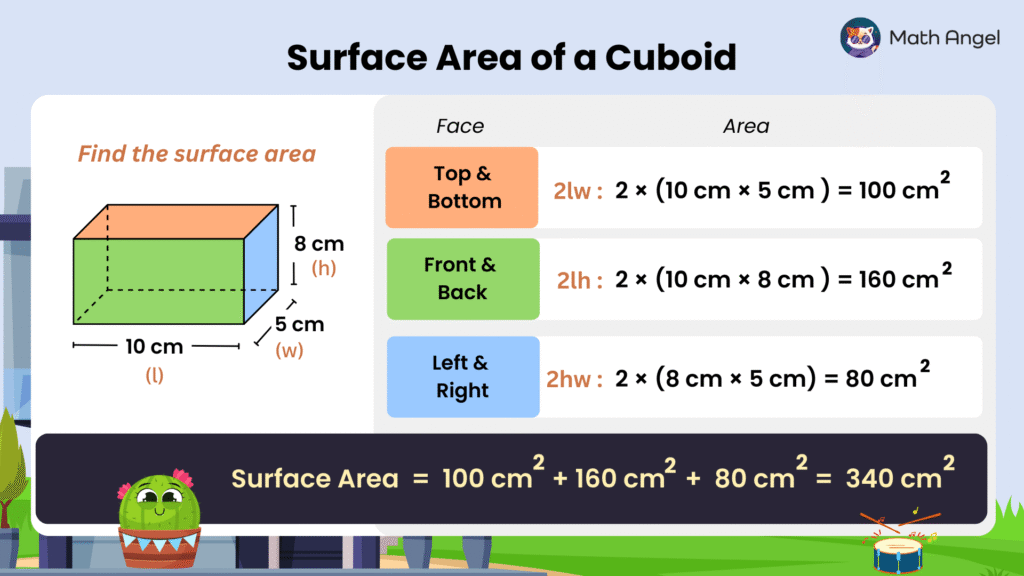
Calculating the Surface Area of a Cuboid
⏩️
A cuboid has:
- Length ($l$) = 10 cm
- Width ($w$) = 5 cm
- Height ($h$) = 8 cm
To find the surface area, calculate the area of each pair of faces and add them up:
- Top + Bottom: $ \quad 2 \times l \times w = 2 \times 10\,\text{cm} \times 5\,\text{cm} = 100\,\text{cm}^2 $
- Front + Back: $ \quad 2 \times l \times h = 2 \times 10\,\text{cm} \times 8\,\text{cm} = 160\,\text{cm}^2$
- Left + Right: $ \quad 2 \times w \times h = 2 \times 5\,\text{cm} \times 8\,\text{cm} = 80\,\text{cm}^2$
Adding them together:
$$ \text{Surface Area} = 100 \text{ cm}^2 + 160\text{ cm}^2 + 80\text{ cm}^2 = 340\text{ cm}^2$$
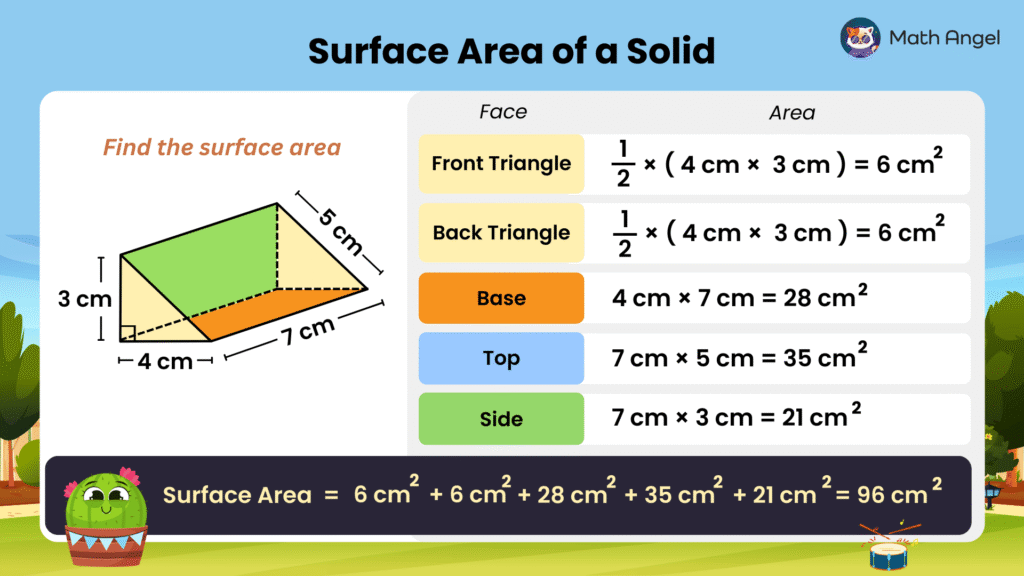
Finding the Surface Area of a Triangular Prism
⏩️
This triangular prism has 5 faces:
- 2 identical triangles (front and back)
- 3 rectangles (base, top, and side)
Let’s find the surface area of this prism step by step:
Front triangle: $\quad \frac{1}{2} \times 4\text{ cm} \times 3\text{ cm} = 6\text{ cm}^2$
Back triangle: $\quad \frac{1}{2} \times 4\text{ cm} \times 3\text{ cm} = 6\text{ cm}^2$
Base rectangle: $\quad 4\text{ cm} \times 7\text{ cm} = 28\text{ cm}^2$
Top rectangle: $\quad 7\text{ cm} \times 5\text{ cm} = 35\text{ cm}^2$
Side rectangle: $\quad 7\text{ cm} \times 3\text{ cm} = 21\text{ cm}^2$
Add all of them together:
$$ \text{Surface Area} = 6\text{ cm}^2 + 6\text{ cm}^2 + 28\text{ cm}^2 + 35\text{ cm}^2 + 21\text{ cm}^2 = 96\text{ cm}^2$$
🍪 Quiz: Practice Finding Surface Area of Cuboids and Prisms
🎩 Stuck on Area Calculations? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

