Polygons and Types of Quadrilaterals
Table Of Contents
🎬 Math Angel Video: Polygon Definition and Properties
What is a Polygon?
⏩️
🛎️ A polygon is a closed, 2D shape made up of straight line segments only.
Examples of Polygons: Triangles, quadrilaterals, pentagons, hexagons, and stars are all polygons because they are closed shapes with only straight sides.
🚨 What is NOT a Polygon?
A shape is not a polygon if it does not meet all three conditions:
- Not 2D: If a shape is three-dimensional (like a cube) or just a single point, it is not a polygon.
- Not Closed: If the shape has gaps and does not fully enclose an area, it is not a polygon.
- Not Straight: If any part of the shape is curved instead of straight, it is not a polygon.
Understanding polygons is important in geometry, as they form the basis of many mathematical concepts and real-world applications.
Common Polygons and Their Names
⏩️
Polygons are classified based on the number of their sides. Here are the names of some common polygons:
- 3-sided polygon → Triangle
- 4-sided polygon → Quadrilateral
- 5-sided polygon → Pentagon
- 6-sided polygon → Hexagon
- 7-sided polygon → Heptagon
- 8-sided polygon → Octagon
- 9-sided polygon → Nonagon
- 10-sided polygon → Decagon
Sum of Interior Angles of Polygons (Formula)
⏩️
The sum of all interior angles in a polygon depends on the number of sides. Here is the formula:
$$ \text{Sum of interior angles} = (n-2) \times 180^\circ $$
where $ n $ is the number of sides.
- Triangle (3 sides): $ \ (3-2) \times 180^\circ = 180^\circ $
- Quadrilateral (4 sides): $ \ (4-2) \times 180^\circ = 360^\circ $
- Pentagon (5 sides): $ \ (5-2) \times 180^\circ = 540^\circ $
- Hexagon (6 sides): $ \ (6-2) \times 180^\circ = 720^\circ $
Understanding this formula helps in geometry when calculating unknown interior angles in polygons.
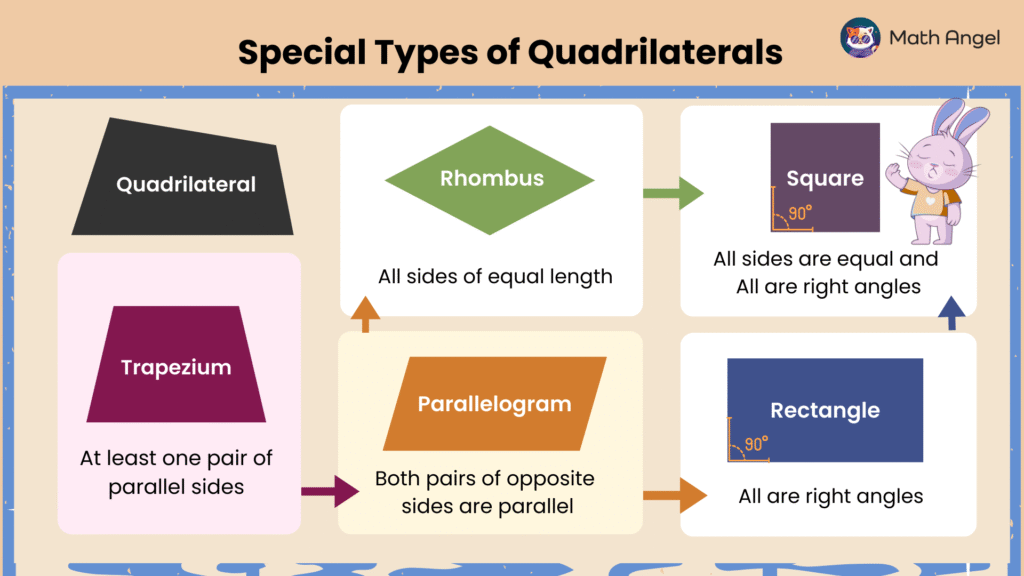
Special Types of Quadrilaterals
⏩️
🛎️ What is a Quadrilateral?
A quadrilateral is a four-sided polygon.
There are different types of quadrilaterals, each with unique properties:
- Trapezium: Has at least one pair of parallel sides.
- Parallelogram: Both pairs of opposite sides are parallel.
- Rhombus: All sides are of equal length.
- Rectangle: Has four right angles.
- Square: All sides are equal, and all angles are right angles.
Understanding these quadrilaterals helps in geometry, construction, and design.
🍪 Quiz: Practice Polygons and Sum of Interior Angles
🎩 Stuck on Shapes and Geometry? Try AI Math Solver
Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.
