Pie Chart

🎬 Video: Pie Chart Concept, Formula, Examples

What is a Pie Chart? (0:01)

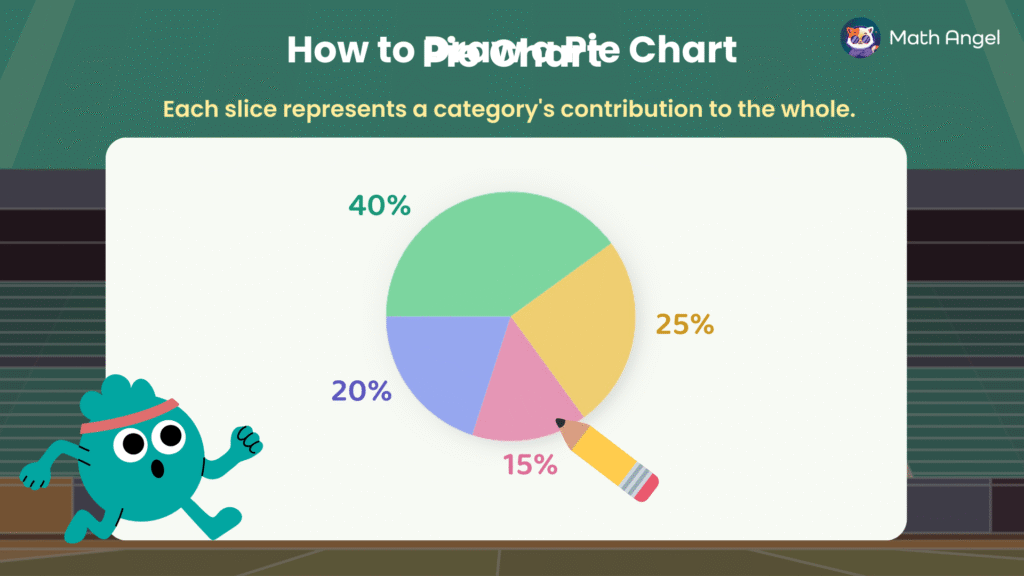
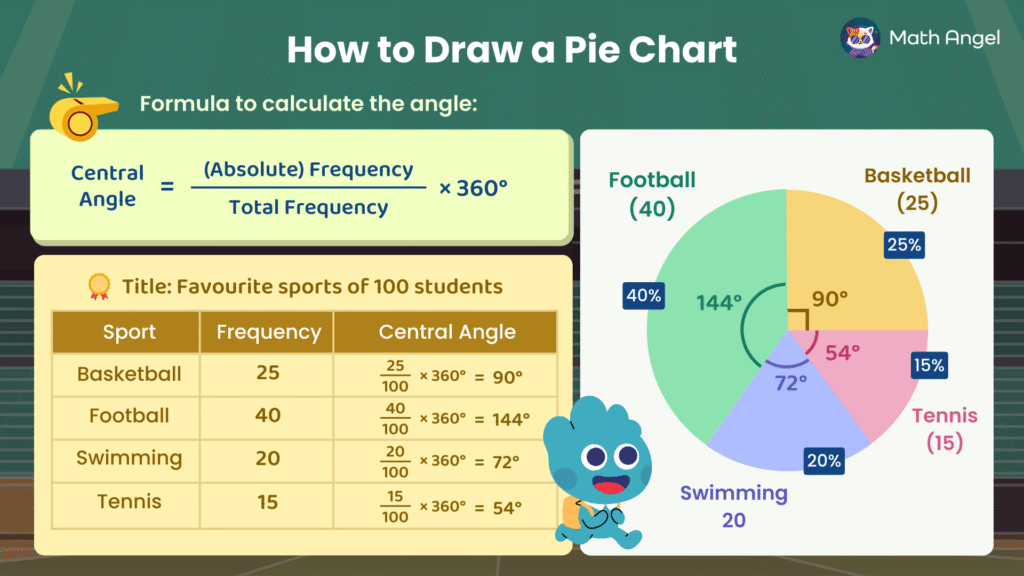
A pie chart is a circular chart that shows how a whole is divided into parts. Each slice represents a category. The size of the slice shows the proportion that category contributes.

✅ Key Characteristics of Pie Charts:

  • The total of all slices is 100%.
  • Each slice shows one category only.
  • Bigger slice = bigger proportion.

💡 Why Use Pie Charts?

  • Show how something is divided
    e.g. How a student’s time is spent in a day: sleeping, school, sports

  • Compare different parts of a whole
    e.g. Favourite school subjects: Maths, Science, English, Art

  • Spot the biggest or smallest category fast
    e.g. Which pet is most popular in a class: dogs, cats, birds, fish

How to Draw a Pie Chart? (0:25)

To draw a pie chart, you need to turn data into angles.

Step 1: Use the formula to calculate central angles:

$$
\text{Central Angle} = \left( \frac{\text{Frequency}}{\text{Total Frequency}} \right) \times 360^\circ
$$

Sport Frequency Central Angle
Basketball 25 (25 ÷ 100) × 360° = 90°
Football 40 (40 ÷ 100) × 360° = 144°
Swimming 20 (20 ÷ 100) × 360° = 72°
Tennis 15 (15 ÷ 100) × 360° = 54°
Total 100 90° + 144° + 72° + 54° = 360°

Step 2: Always check your angles add up to 360° and your percentages add up to 100%.

Step 3: Use a protractor to mark each angle carefully.

Step 4: Label each slice with the sport and percentage.

How to Read a Pie Chart? (2:20)

A pie chart doesn’t just show you percentages — it can also help you work out actual numbers and find hidden data.

✅ Formula to Find the Frequency (Count) of a Category:

$$
\text{Count of the Category} = \left( \frac{\text{Central Angle}}{360^\circ} \right) \times \text{Total Count}
$$

🍕 Pie Chart Example: Favourite Pizza Toppings of Students

We are given: 

  • Pepper = 90°, corresponding to 20 students.
  • Mushroom = 162°
  • Ham = 36°
  • Pineapple = unknown


1) How many students took the survey?

We’re told that 90° represents 20 students (Pepper).

  • Use the formula:

$$
\frac{90^\circ}{360^\circ} \times \text{Total} = 20
$$

  • Solving for Total:

$$
\text{Total} = 80 \text{ students}
$$

2) How many students prefer ham topping?

  • Ham = 36°, total students = 80

$$
\frac{36^\circ}{360^\circ} \times 80 = \frac{1}{10} \times 80 = 8 \text{ students}
$$

3) What percentage of students like pineapple?

  • Pineapple angle is calculated as:

$$
360^\circ – 90^\circ – 162^\circ – 36^\circ = 72^\circ
$$

  • The percentage of students who prefer pineapple:

$$
\frac{72^\circ}{360^\circ} \times 100\% = 20\%
$$

📂 Flashcards: How to Draw and Read a Pie Chart

A pie chart divided into four sections, labelled 40%, 25%, 20%, and 15%, representing different category contributions.
1) What is A Pie Chart?
Pie chart of favourite sports of 100 students, football (40%), basketball (25%), swimming (20%), and tennis (15%). Central angle formula is displayed.
2) How to Draw A Pie Chart
A visual guide on how to read a pie chart, with a formula for calculating category counts.
3) How to Read a Pie Chart

🍪 Quiz: Practice Reading and Interpreting Pie Charts

0%

Pie Chart

1 / 6

Q: The pie chart shows the favourite genres of movies among 80 students. How many students prefer Comedy?

Pie chart divided into four sections labelled Comedy, Drama, Horror, and Action, with inner angles of 90°, 90°, 60°, and 120° respectively.

2 / 6

Q: The table below shows favourite outdoor activities among students. What is the central angle for Cycling?

A table showing activities (Hiking, Cycling, Running, Swimming) and their respective number of students: 30, 20, 10, and 40, for calculating angles in a pie chart.

3 / 6

Q: The table below shows the favourite colours of 50 students. What is the central angle for Blue?

A table showing colours (Red, Blue, Green, Yellow) and their respective number of students: 15, 20, 10, and 5, for calculating angles in a pie chart.

4 / 6

Q: The table below shows students' favourite ice cream flavours. What is the central angle for Strawberry?

A table showing flavours (Chocolate, Vanilla, Strawberry, Mint) and their respective number of students: 30, 20, 25, and 25, for calculating angles in a pie chart.

5 / 6

Q: The pie chart shows the time spent on different activities during the day. What is the total time spent on Studying if the total hours in a day are 24?

Pie chart divided into sections labelled Sleeping, Free Time, Studying, and Eating, with angles of 180°, 90°, 60°, and 30° respectively.

6 / 6

Q: A pie chart shows the favourite sports of students at a school. If 60 students prefer Basketball, how many students perfer volleyball?

Pie chart divided into sections labelled Volleyball, Badminton, Tennis, and Basketball, with angles of 120°, 90°, 90°, and 60° respectively.

Your score is

The average score is 36%

0%

🎩 Stuck on Pie Charts or Data? Try AI Math Solver

Need math help? Chat with our AI Math Solver at the bottom right — available 24/7 for instant answers.

Previous Lesson
Back to Course
Next Lesson
12 Comments
5 2 votes
Article Rating
guest
12 Comments
Newest
Oldest Most Voted
Inline Feedbacks
View all comments

Leave a Comment

Your email address will not be published. Required fields are marked *