Probability and Statistics

Probability

Calculating Probability

Addition Rule of Probability and Expected Frequency

Probability Tree Diagrams

Sets and Venn Diagrams

Statistics

Tally Marks, Bar Charts, Tables

Absolute Frequency and Relative Frequency

How to Calculate the Mean, Median, Mode, and Range

Median, Mean, Mode, Range from a Frequency Table

Averages from Grouped Frequency Table

How to Draw and Read a Box Plot

Line Graphs and Curve Graphs

Previous Lesson

{results_count} Math videos for {phrase}

Displaying {results_count} results of {results_count_total}

Generic filters

Exact matches only

Search in title

Search in content

Search in excerpt

Filter by Lesson Categories

Addition Rule of Probability and Expected Frequency

Probability and Statistics Addition Rule of Probability and Expected Frequency

Courses Overview

🎬 Video Tutorial

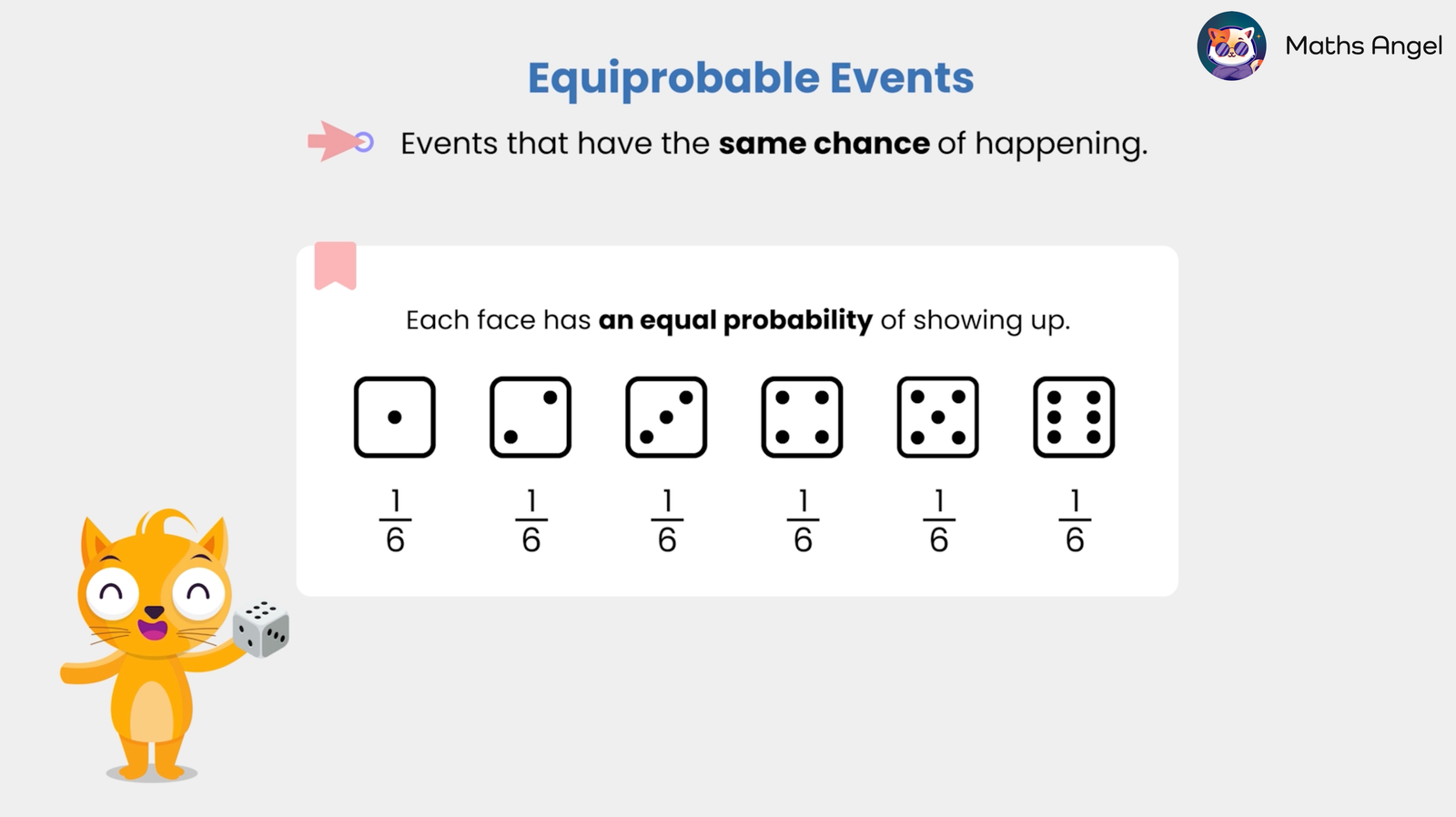
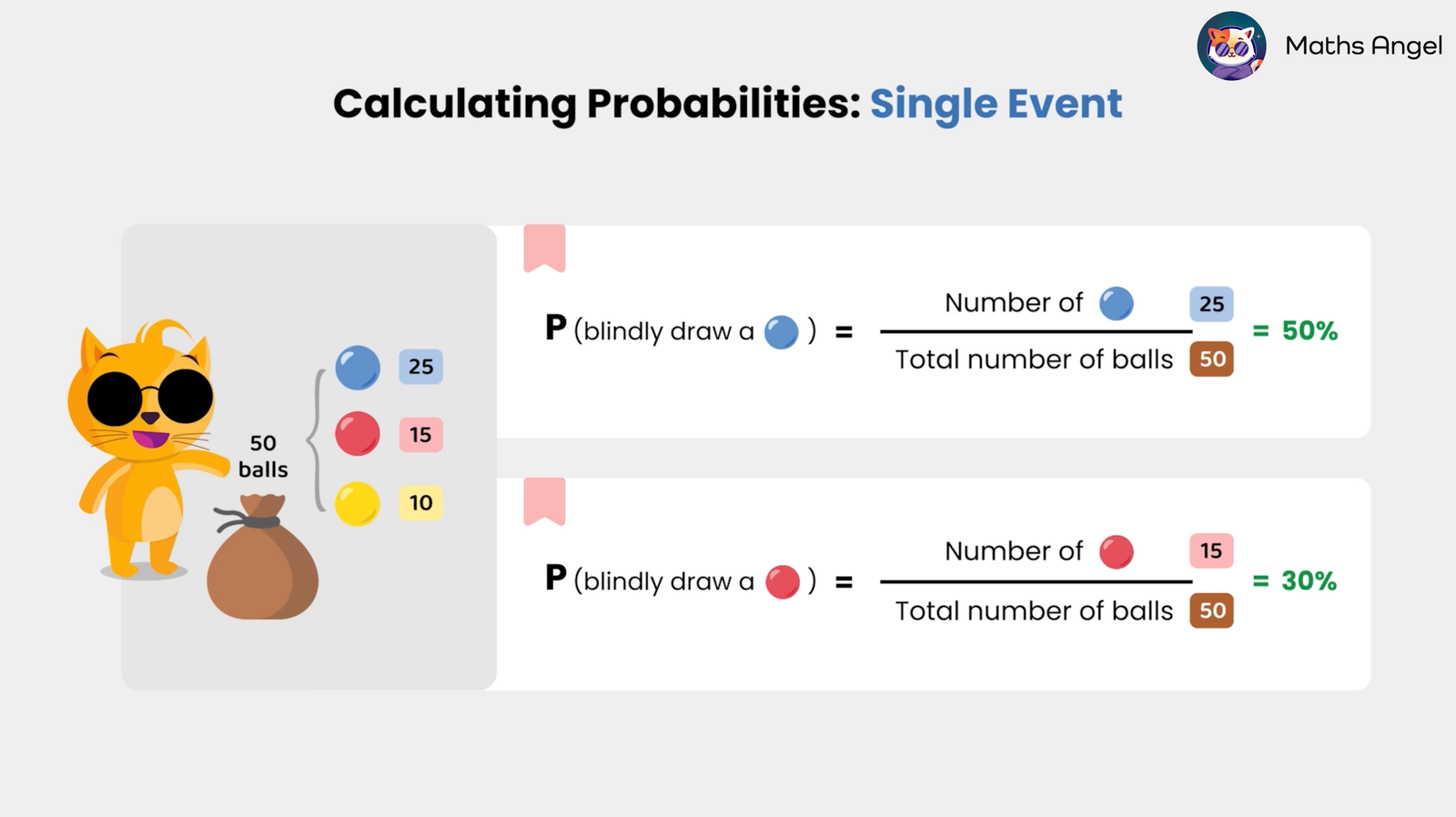
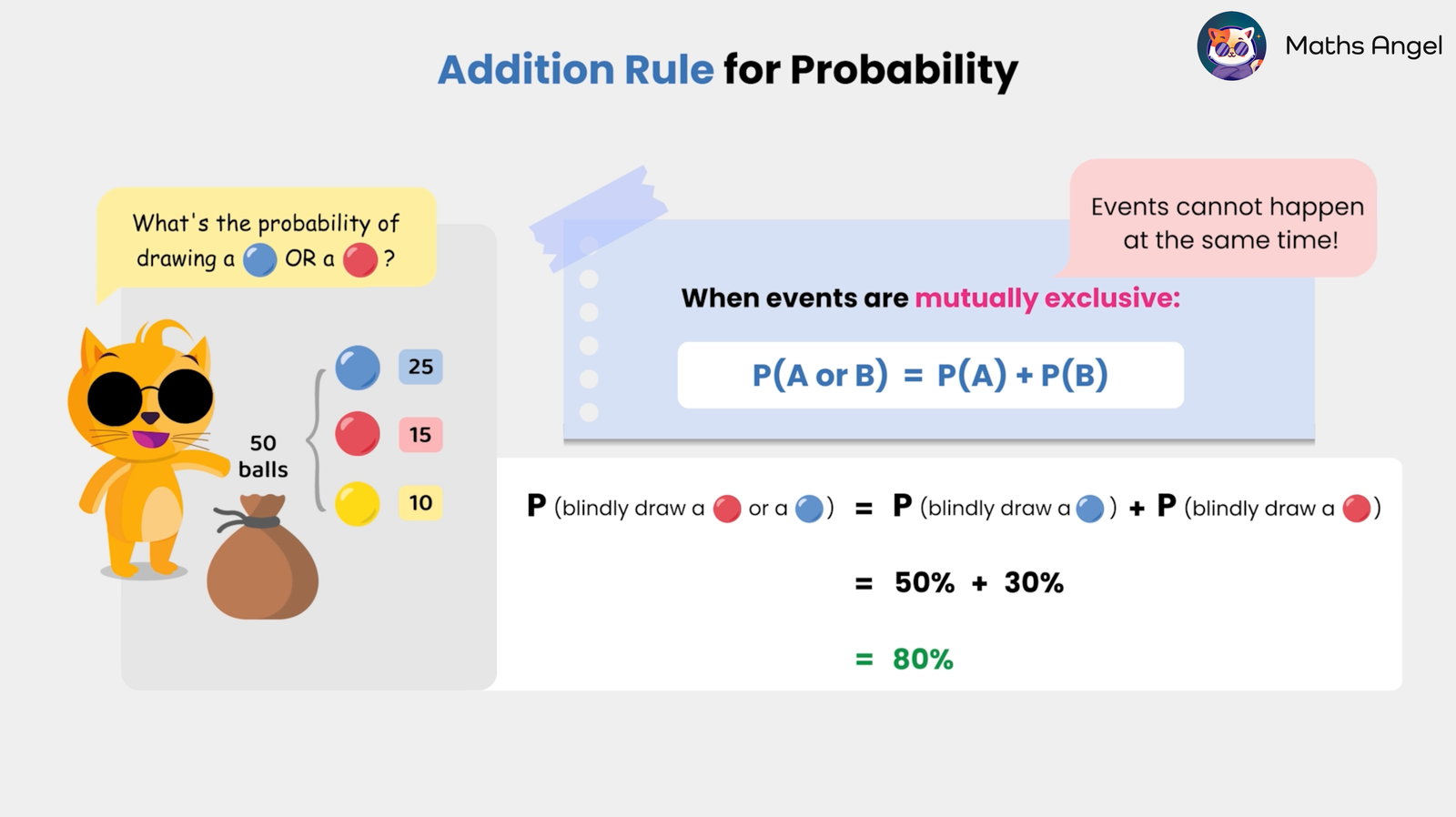
(0:01) What are Equiprobable Events? Equiprobable events are events with equal chances of occurring. For example, when rolling a fair six-sided die, each face has a probability of $\frac{1}{6}$ of landing face-up.
(0:25) How to Calculate the Probability of Single Events? Probability is found by dividing the number of favourable outcomes by the total number of possible outcomes. For example, if a bag contains 50 balls (25 blue, 15 red, and 10 yellow), the probability of randomly drawing a blue ball is $ \frac{25}{50} = 50\text{%} $, and the probability of drawing a red ball is $ \frac{15}{50} = 30\text{%} $.
(1:32) What is the Addition Rule of Probability? When events are mutually exclusive (meaning they cannot happen at the same time), the probability of $A$ or $B$ is the sum of their individual probabilities. For example, the probability of drawing a blue or red ball is $ P(\text{Blue or Red}) = P(\text{Blue}) + P(\text{Red})$ = $50\text{%} + 30\text{%} = 80\text{%} $.
(2:23) Understanding Expected Frequency: Expected absolute frequency tells us how often we expect an event to occur over a number of trials. For example, when rolling a fair six-sided die $60$ times, the probability of rolling a 3 is $ \frac{1}{6} $, so the expected frequency is $ \left( \frac{1}{6} \right) \times 60 = 10 $ times. However, since “expected” is just an estimation, actual results may vary.

📂 Revision Cards

Explanation of equiprobable events by using a die and showing that each face has an equal probability of 1/6. — 1) What are Equiprobable Events?

Drawing coloured balls from a bag with 50 balls, showing 50% for blue and 30% for red. — 2) Calculating Probability of Single Events

Explanation of the probability of drawing blue or red balls from a bag with 50 balls using the addition rule of probability for mutually exclusive events. — 3) Addition Rule of Probability

Calculating the expected absolute frequency using a die, illustrating that the expected absolute frequency of rolling a "3" over 60 trials is 10. — 4) Expected Absolute Frequency

🍪 Quiz

0%

Probability Rules and Expected Values

1 / 6

Q: In a bag with 50 balls, there are 25 blue, 15 red, and 10 yellow balls. What is the probability of drawing a yellow ball?

$\frac{3}{5}$

$\frac{2}{5}$

$\frac{1}{5}$

$\frac{35}{50}$

Feedback: Not quite! There are 10 yellow balls out of a total of 50. The probability of drawing a yellow ball is $\frac{10}{50}$, which simplifies to $\frac{1}{5}$.

Feedback: Well done! There are 10 yellow balls out of a total of 50. The probability of drawing a yellow ball is $\frac{10}{50}$, which simplifies to $\frac{1}{5}$.

2 / 6

Q: If you roll a fair six-sided die, what is the probability of rolling either a 2 or a 6?

$\frac{1}{3}$

$\frac{1}{2}$

$\frac{1}{6}$

$\frac{6}{6}$

Feedback: Not quite! There are two favourable outcomes (rolling a 2 or a 6) out of 6 possible outcomes. Therefore, the probability is $\frac{2}{6}$, which simplifies to $\frac{1}{3}$.

Feedback: Well done! There are two favourable outcomes (rolling a 2 or a 6) out of 6 possible outcomes. Therefore, the probability is $\frac{2}{6}$, which simplifies to $\frac{1}{3}$.

3 / 6

Q: A box contains 15 red, 5 blue, and 10 green marbles. What is the probability of drawing a red or green marble?

$\frac{5}{6}$

$\frac{1}{2}$

$\frac{1}{6}$

$\frac{1}{3}$

Feedback: Not quite! The total number of red and green marbles is 15 (red) + 10 (green) = 25 marbles. The total number of marbles is 30. The probability of drawing a red or green marble is $\frac{25}{30}$, which simplifies to $\frac{5}{6}$.

Feedback: Well done! The total number of red and green marbles is 15 (red) + 10 (green) = 25 marbles. The total number of marbles is 30. The probability of drawing a red or green marble is $\frac{25}{30}$, which simplifies to $\frac{5}{6}$.

4 / 6

Q: A bag contains 6 red, 4 blue, and 2 yellow marbles. What is the probability of drawing a yellow or blue marble?

$\frac{1}{2}$

$\frac{5}{12}$

$\frac{2}{3}$

$\frac{10}{12}$

Feedback: Not quite! The total number of yellow and blue marbles is 4 (blue) + 2 (yellow) = 6 marbles. The total number of marbles is 12. So, the probability of drawing a yellow or blue marble is $\frac{6}{12}$, which simplifies to $\frac{1}{2}$.

Feedback: Well done! The total number of yellow and blue marbles is 4 (blue) + 2 (yellow) = 6 marbles. The total number of marbles is 12. So, the probability of drawing a yellow or blue marble is $\frac{6}{12}$, which simplifies to $\frac{1}{2}$.

5 / 6

Q: You roll a fair die 60 times. How many times would you expect to roll a 3?

15

12

18

10

Feedback: Not quite! The probability of rolling a 3 on a fair die is $\frac{1}{6}$. If you roll the die 60 times, the expected number of 3s is $\frac{1}{6} \times 60 = 10$.

Feedback: Well done! The probability of rolling a 3 on a fair die is $\frac{1}{6}$. If you roll the die 60 times, the expected number of 3s is $\frac{1}{6} \times 60 = 10$.

6 / 6

Q: You roll a fair die 120 times. How many times would you expect to roll a number less than 3?

40

60

20

80

Feedback: Not quite! The probability of rolling a number less than 3 (either 1 or 2) is $\frac{2}{6}$, which simplifies to $\frac{1}{3}$. So if you roll the die 120 times, you would expect $\frac{1}{3} \times 120 = 40$ rolls to be less than 3. Note that this is an estimate, the actual number might be a bit higher or lower.

Feedback: Well done! The probability of rolling a number less than 3 (either 1 or 2) is $\frac{2}{6}$, which simplifies to $\frac{1}{3}$. So if you roll the die 120 times, you would expect $\frac{1}{3} \times 120 = 40$ rolls to be less than 3. Note that this is an estimate, the actual number might be a bit higher or lower.

Your score is

The average score is 56%

0%

🎩 AI Math Solver (ChatCat)

Need math help? Chat with our AI Math Solver at the bottom right!

Previous Lesson

0 0 votes

Article Rating

Label

Name*

Email

Label

Name*

Email

0 Comments

Newest

Oldest Most Voted

Inline Feedbacks

View all comments

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Comment *

Name

Email

Website

Save my name, email, and website in this browser for the next time I comment.

Log In

Username or Email Address

Password

Remember Me

Join Now | Lost Password?

Login

Accessing this course requires a login. Please enter your credentials below!

Username or Email Address

Password

Remember Me

Lost Your Password?

Register

Don't have an account? Register one!

Register an Account