Circumference and Area of a Circle and a Sector
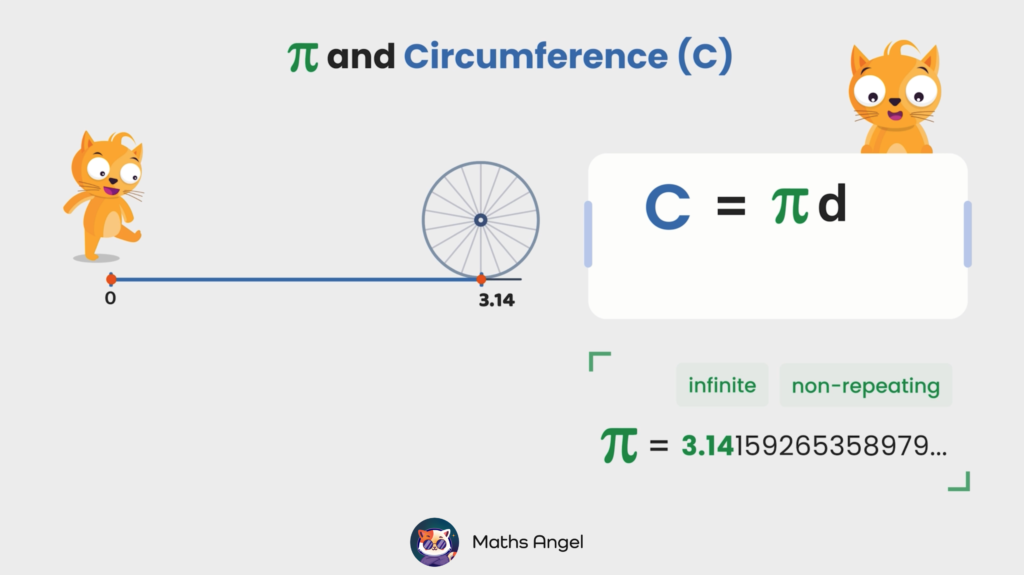
Open to access this content
Perpendicular and Parallel Lines
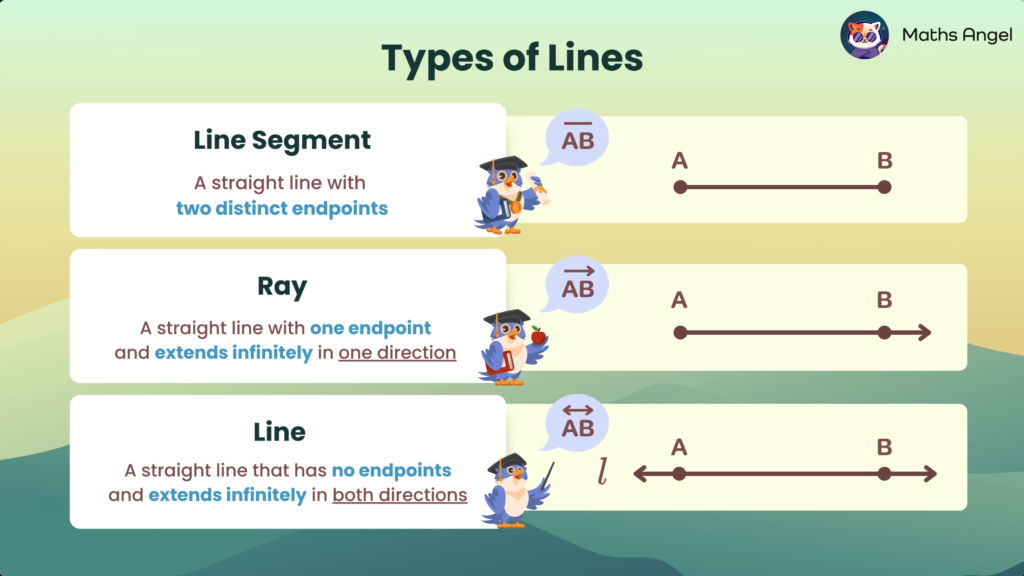
Open to access this content
Volume and Surface Area of Pyramids, Cones, Spheres
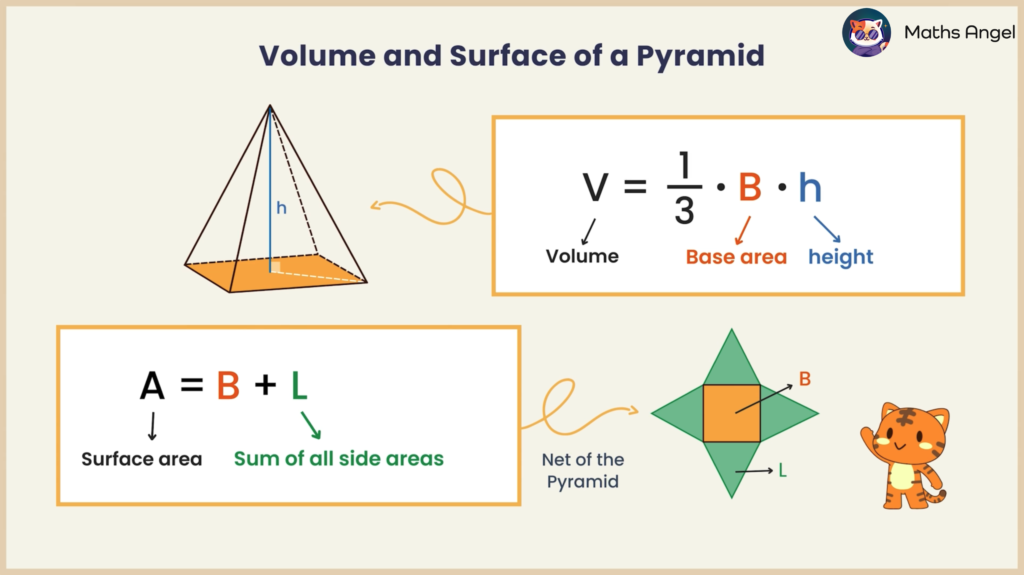
Open to access this content
Perimeter of a Polygon
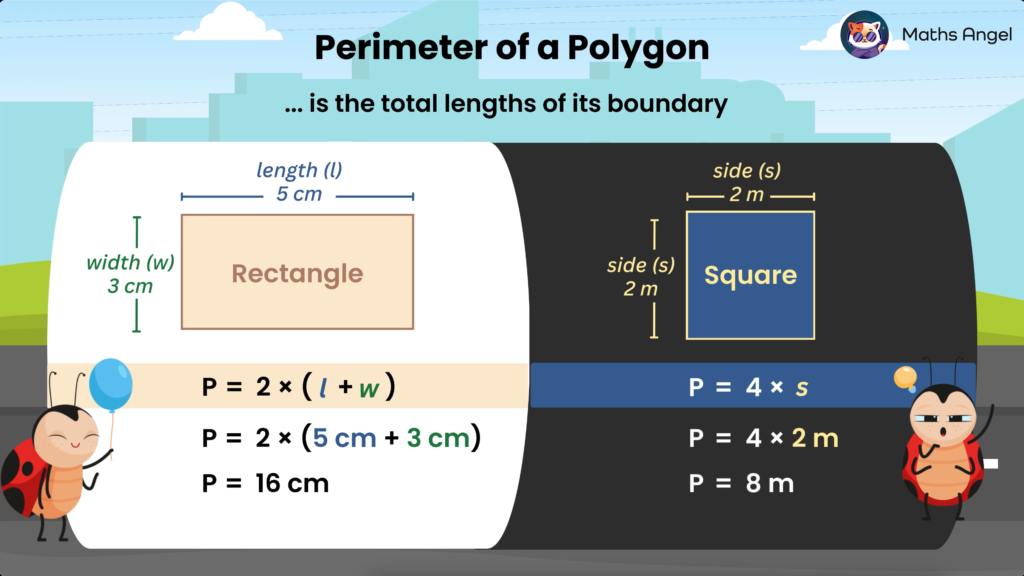
Open to access this content
Area of Parallelograms and Triangles
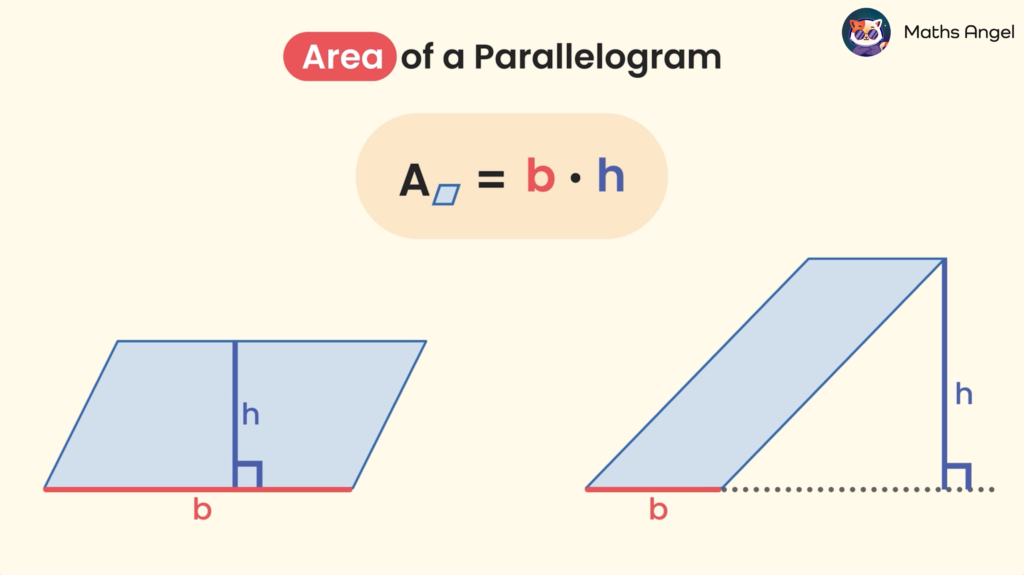
Open to access this content
Volume of a Cuboid and Cube
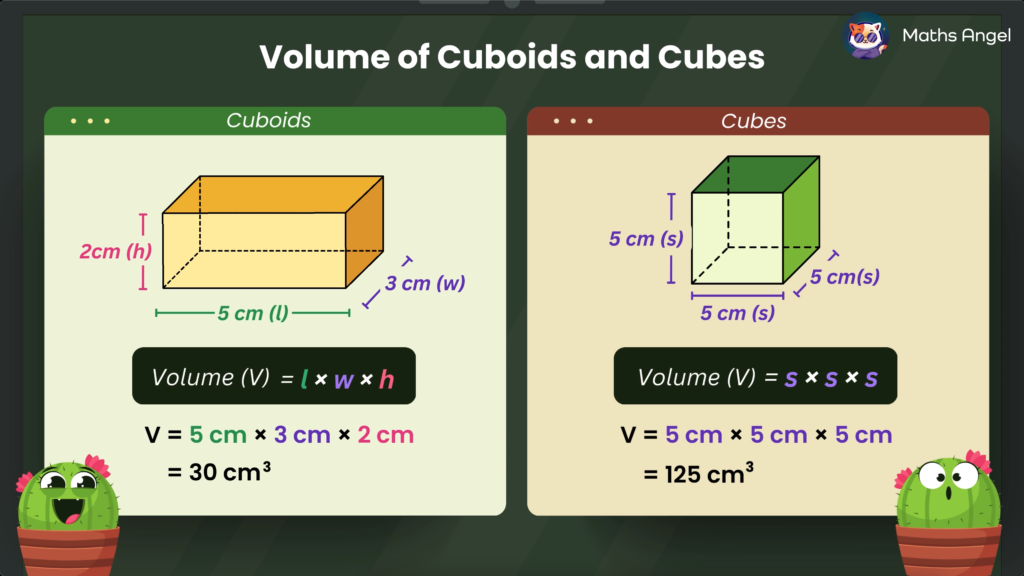
Open to access this content
Surface Area of Solids
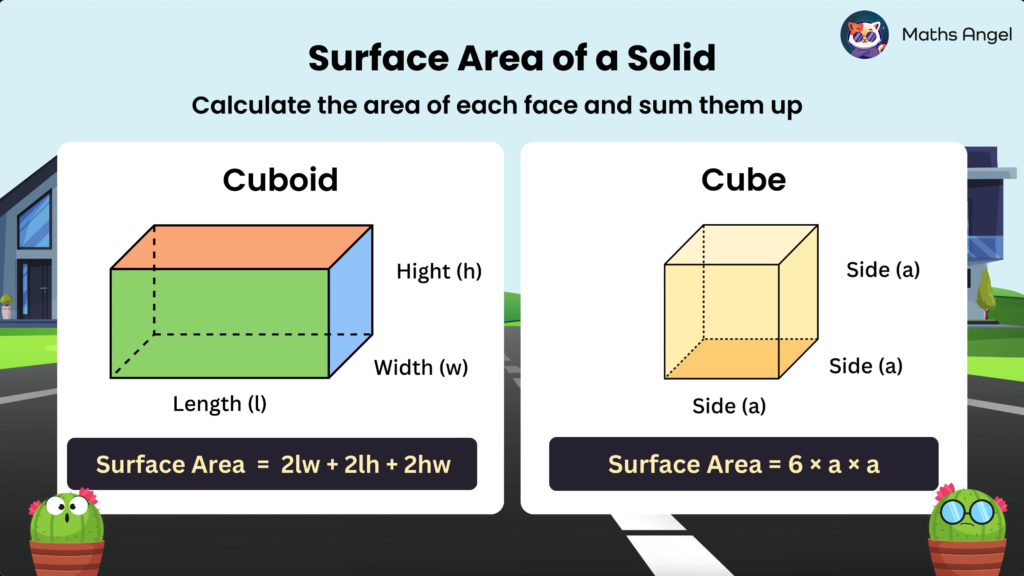
Open to access this content
Volume of Prisms and Cylinders
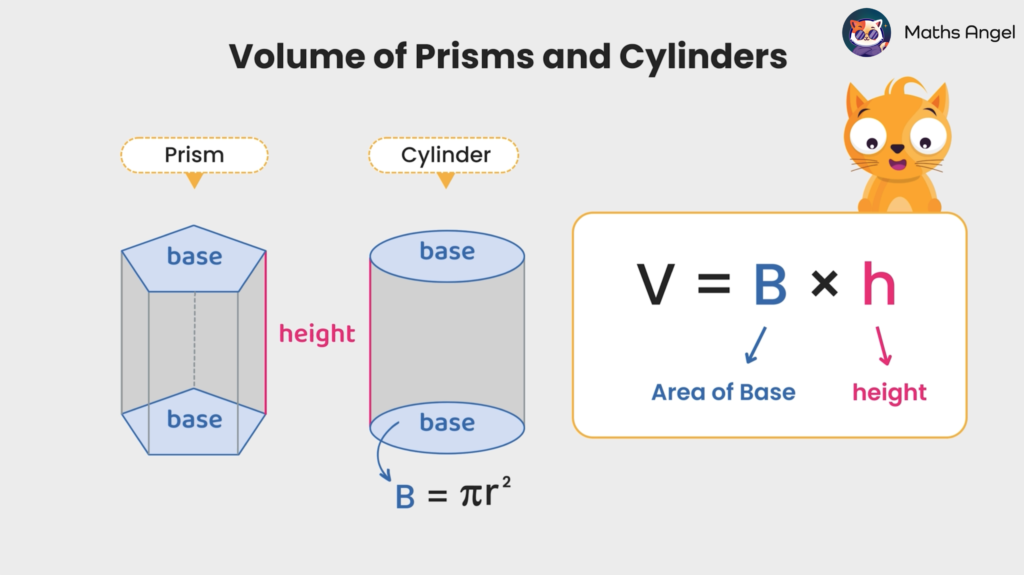
Open to access this content
Cavalieri’s Principle
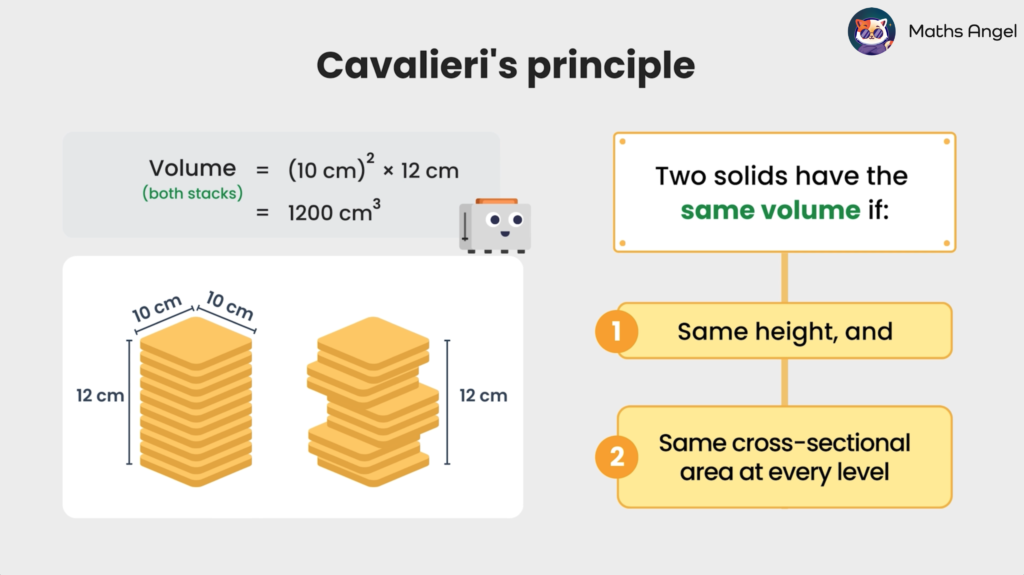
Open to access this content
Perpendicular Bisectors and Circumcircle
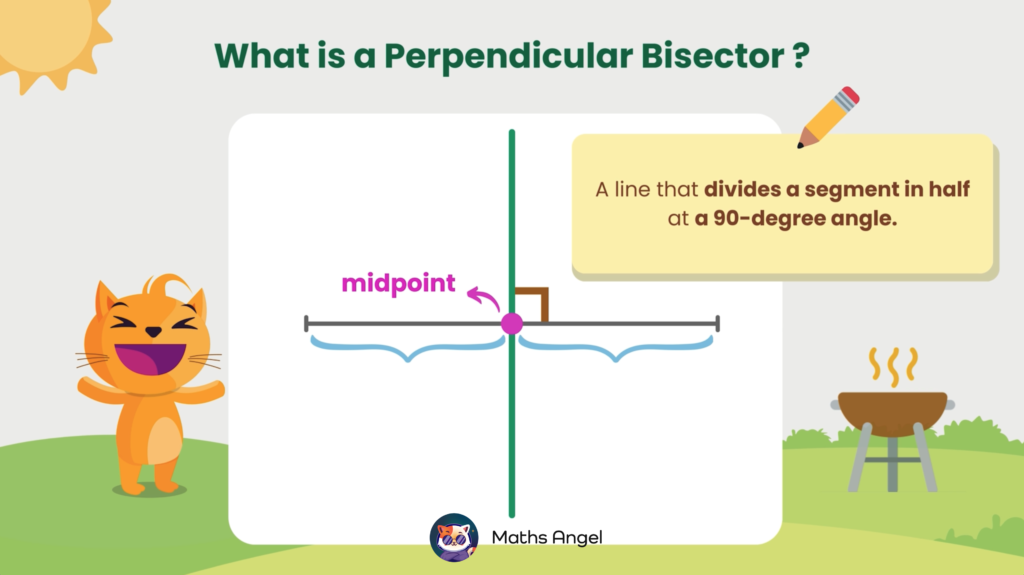
Open to access this content
